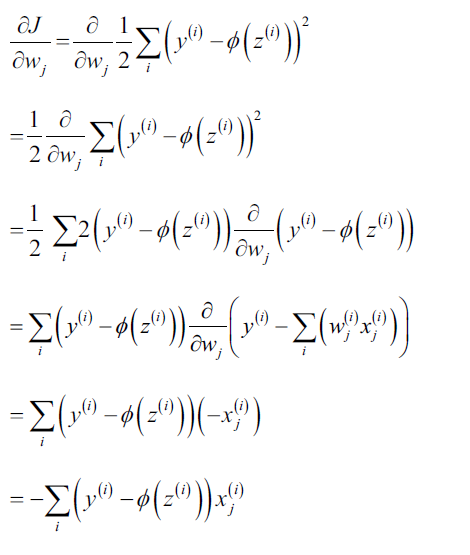自适应线性神经元及收敛问题

本节我们学习另一种单层神经网络：自适应线性神经元(ADAptive LInear NEuron, 简称Adaline)。在Frank Rosenblatt提出感知计算法不久，Bernard Widrow和他的博士生Tedd Hoff提出了Adaline算法作为感知机的改进算法(B.Widrow et al. Adaptive "Adaline" neuron using chemical "memistors".)

相对于感知机，Adaline算法有趣的多，因为在学习Adaline的过程中涉及到机器学习中一个重要的概念：定义、最小化损失函数。学习Adaline为以后学习更复杂高端的算法(比如逻辑斯蒂回归、SVM等)起到抛砖引玉的作用。

Adaline和感知机的一个重要区别是Adaline算法中权重参数更新按照线性激活函数而不是单位阶跃函数。当然，Adaline中激活函数也简单的很，。

虽然Adaline中参数更新不是使用阶跃函数，但是在对测试集样本输出预测类别时还是使用阶跃函数，毕竟要输出离散值-1,1。

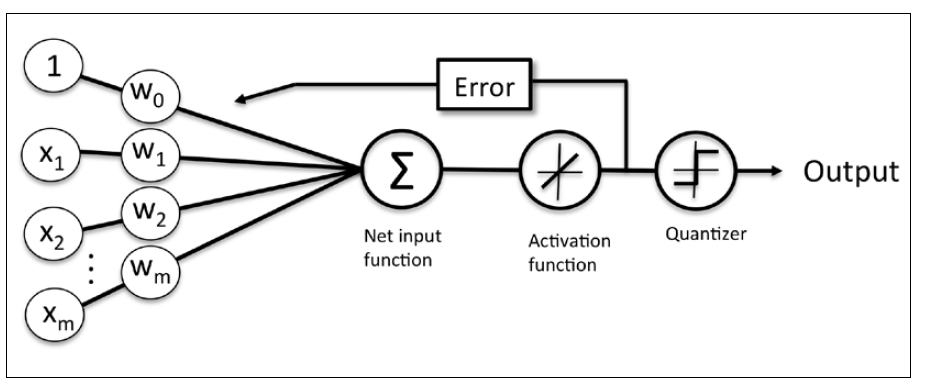
使用梯度下降算法最小化损失函数

在监督机器学习算法中，一个重要的概念就是定义目标函数(objective function)，而目标函数就是机器学习算法的学习过程中要优化的目标，目标函数我们常称为损失函数(cost function)，在算法学习(即，参数更新)的过程中就是要最小化损失函数。

对于Adaline算法，我们定义损失函数为样本真实值和预测值之间的误差平方和(Sum of Squared Erros, SSE):

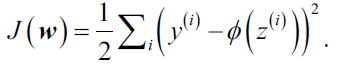
上式中的系数完全是为了求导数方便而添加的，没有特殊的物理含义。相对于感知机中的单位阶跃函数，使用连续现行激活函数的一大优点是Adaline的损失函数是可导的。另一个很好的特性是Adaline的损失函数是凸函数，因为，我们可以使用简单而有效的优化算法：梯度下降(gradient descent)来找到使损失函数取值最小的权重参数。

如下图所示，我们可以把梯度下降算法看做"下山",直到遇到局部最小点或者全局最小点才会停止计算。在每一次迭代过程中，我们沿着梯度下降方向迈出一步，而步伐的大小由学习率和梯度大小共同决定。

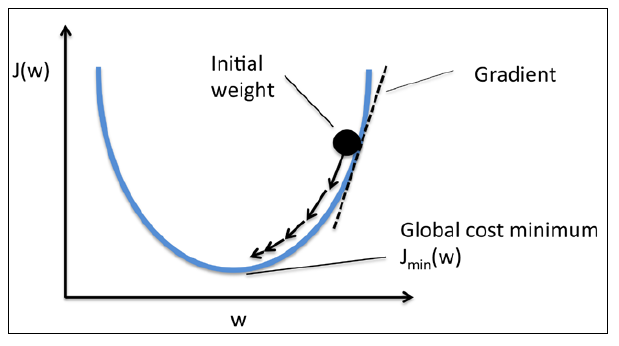
使用梯度下降算法，实质就是运用损失函数的梯度来对参数进行更新：

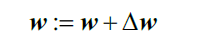
此时，的值由负梯度乘以学习率确定：

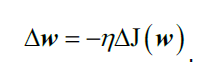
而要计算出损失函数的梯度，我们需要计算损失函数对每一个权重参数的偏导数:

因此，.

注意所有权重参数还是同时更新的，所以Adaline算法的学习规则可以简写: .

虽然简写以后的学习规则和感知机一样，但不要忘了的不同。此外，还有一点很大的不同是在计算权重更新的过程中：Adaline需要用到所有训练集样本才能一次性更新所有的w，而感知机则是每次用一个训练集样本更新所有权重参数。所以梯度下降法常被称为批量梯度下降 ("batch" gradient descent)。

福利： 详细的损失函数对权重的偏导数计算过程为：