选择有意义的特征
如果一个模型在训练集的表现比测试集好很多,那我们就要小心了,模型很可能过拟合了。过拟合意味着模型捕捉了训练集中的特例模式,但对未知数据的泛化能力比较差,我们也说模型此时具有高方差。
模型过拟合的一个原因是对于给定的训练集数据,模型过于复杂,常用的减小泛化误差的做法包括:
- 收集更多的训练集数据
- 正则化,即引入模型复杂度的惩罚项
- 选择一个简单点的模型,参数少一点的
- 降低数据的维度
在上面的一系列做法中,第一条收集更多数据通常不实用。在下一章,我们会学习一个有用的技巧来判断更多的训练集数据是否有帮助。在接下来的章节,我们学习正则化和特征选择的方法来降低过拟合。
L1正则
会议第三章,我们运用过L2正则来降低模型的复杂度,当时我们定义的L2正则项:
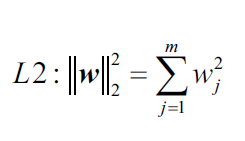
除了L2正则,另一个中减低模型复杂度的方法是L1正则(L1 regularization):
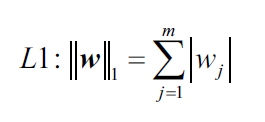
L2正则项是权重参数的平方和,而L1正则项是权重参数的绝对值和。相对于L2, L1正则项趋向于得到稀疏特征向量,即很多特征权重参数为0.如果数据集的特征维度很高且特征不相干(极端情况是 不相干的特征维度数目比训练样本数还大),特征稀疏性是非常有用的。 由于很多特征权重为0,所以,很多人也把L1正则看做特征选择的一种方式。
为了更好地理解L1正则倾向于产生稀疏特征,让我们看一下正则化的几何解释。假设损失函数是差平方损失函数(sum of the squared errors, SSE),且只含有两个权重参数,易知损失函数是凸函数。对于给定的损失函数,我们的目的是找到损失函数取最小值时对应的权重值,如下图损失函数等高线所示,当(
)取椭圆中心点时,损失函数值最小:
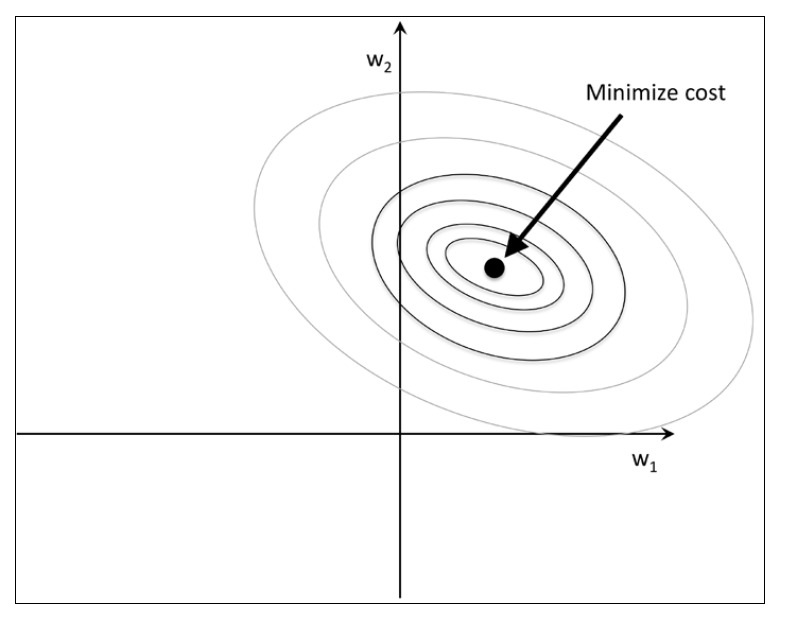
而正则项是对现在损失函数的惩罚项,它鼓励权重参数取小一点的值,换句话说,正则项惩罚的是大权重参数。
因此,如果增大正则系数的值,也就增大了正则项的威力,也就会导致权重参数变小(趋向于0),从而也减小了模型对训练数据的依赖。我们在下图画出L2惩罚项:
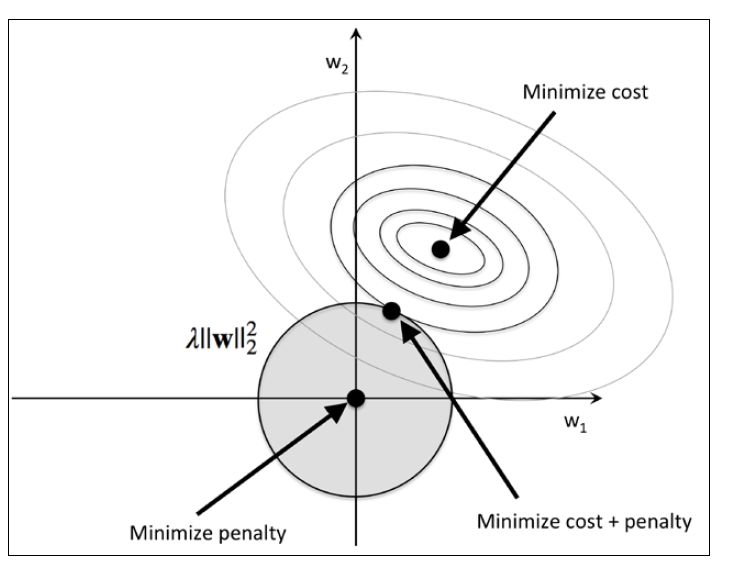
L2正则项用图上阴影球形表示。正则化后的 新损失函数=原始损失函数+正则项,我们可以换一种思路解释这个公式,新的损失函数还是原始损失函数,我们把正则项看做权重参数的限制条件,也就是说,权重参数的取值范围必须在图中阴影球形内。如果增大
的值,会缩小阴影球形面积。比如,如果
趋向正无穷,则阴影面积趋向0,权重参数也趋向0.
我们总结一下:我们的目标是最小化原始损失函数和正则项,等价于在原始损失函数基础上增加限制条件,更加偏向于简单模型来减小方差。
现在我们讨论L1正则项和稀疏性。L1正则和刚才讨论的L2正则很像。当然区别还是有的:L1正则是权重参数绝对值的和,我们用一个另行区域表示,如下图所示:
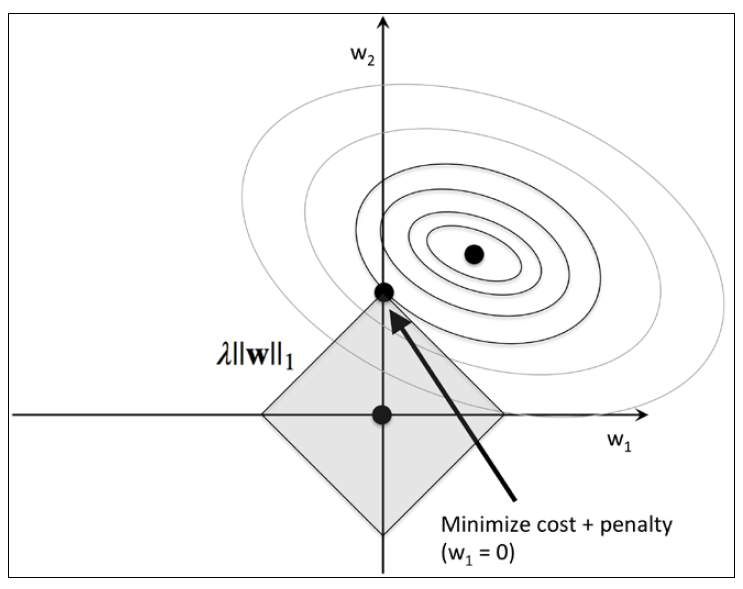
由于菱形的特点,在和损失函数等高线相交时,最小点很可能落在坐标轴上,这就导致了特征的稀疏性。如果你对这背后的数学感兴趣,推荐阅读 The Elements of Statistical Learning, Trevor Hastie, Robert Tibshirani, and Friedman, Springer。
对于sklearn中那些支持L1正则的模型,我们只需要在初始化时用penalty参数设置为L1正则即可:
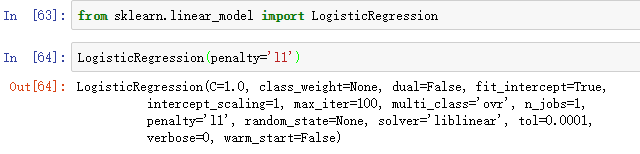
将L1正则逻辑斯蒂回归应用到标准化后的Wine数据集:
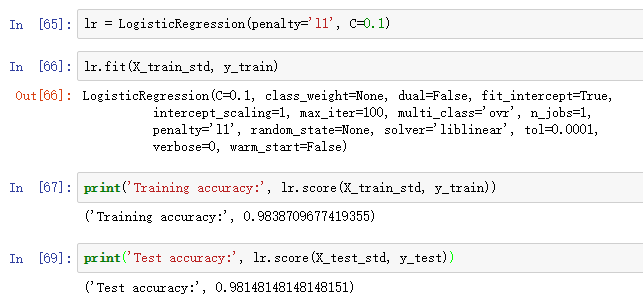
模型在训练集和测试集上的准确率说明没有过拟合。如果我们调用lr.intercept_属性,可以发现只返回了三个值:

由于Wine数据集是多类别数据,所以lr使用了One-vs-Rest(OvR)方法,所以上面三个值分别属于三个模型:第一个模型用类别1 vs 类别2和3;第二个模型用类别2 vs 类别1和3;第三个模型用类别3 vs 类别1和2。
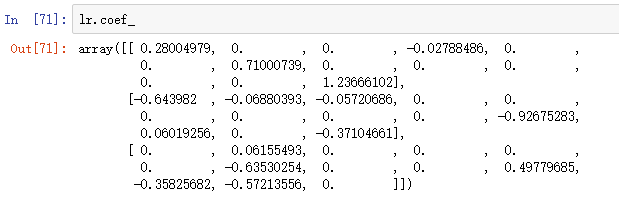
通过lr.coef_得到权重数组,共三行,每一个类对应一行。每一行有13个参数,对应13个特征。网络输入计算如下:
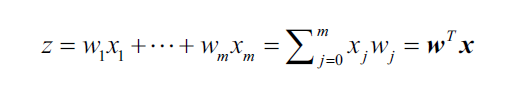
我们可以发现权重向量中有很多0值,这说明L1正则可以作为特征选择的一种手段,得到的模型具有鲁棒性。
最后,我们画出正则路径,即不同正则威力下的不同特征的权重参数:
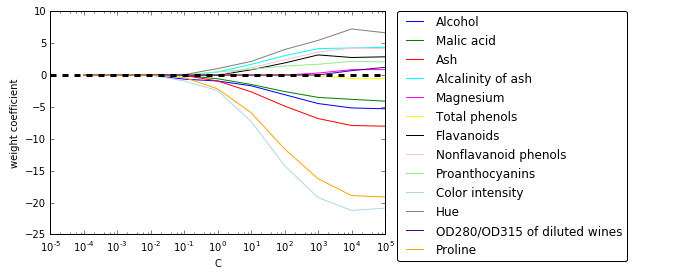
我们可以发现,如果C<0.1,正则项威力很大时,所有特征权重都为0,。
序列特征选择算法
另一种减小模型复杂度和避免过拟合的方法是通过特征选择进行维度降低(dimensionality reduction),这个方法尤其对非正则模型有用。维度降低有两种做法:特征选择(feature selection)和特征抽取(feature extraction)。
特征选择会从原始特征集中选择一个子集合。特征抽取是从原始特征空间抽取信息,从而构建一个新的特征子空间。本节,我们学习特征选择算法。在下一章,我们会学到不同的特征抽取方法来将数据集压缩到一个低维度特征子空间。
序列特征选择算法属于贪心搜索算法,用于将原始的d维度特征空间降低到k维度特征子空间,其中k<d。
特征选择算法的原理是自动选择一个特征子集,子集中的特征都是和问题最相关的特征,这样能够提高计算效率并且由于溢出了不相干特征和噪音也降低了模型的泛化误差。
一个经典的序列特征选择算法是序列后向选择(sequential backward selection, SBS),它能够降低原始特征维度提高计算效率,在某些情况下,如果模型过拟合,使用SBS后甚至能提高模型的预测能力。
Note贪心算法在每一次选择时都会做出局部最优选择,通常产生一个次优全局解,暴力搜索要考虑所有的可能的情况所以会保证得到全局最优解。但由于穷搜的计算复杂度过高,导致其并不是最佳选择。
SBS算法的idea很简单:SBS序列地从原始特征集中移除特征,直到新的特征集数目达到事先确定的值。而在移除特征时,我们需要定义评价函数。一个特征的重要性就用特征移除后的评价函数值表示。我们每一次都把那些评价函数值最大的特征移除,也就是那些对评价函数影响最小的特征去掉。所以,SBS算法有以下4个步骤:
- 1 初始化k=d,其中d是原始特征维度。
- 2 确定那个评价函数最大的特征
。
- 3 从
中移除特征
, k=k-1。
- 4 如果k等于事先确定的阈值则终止;否则回到步骤2。
不过,sklearn目前并没有实现SBS算法,好在算法简单,我们可以自己实现:
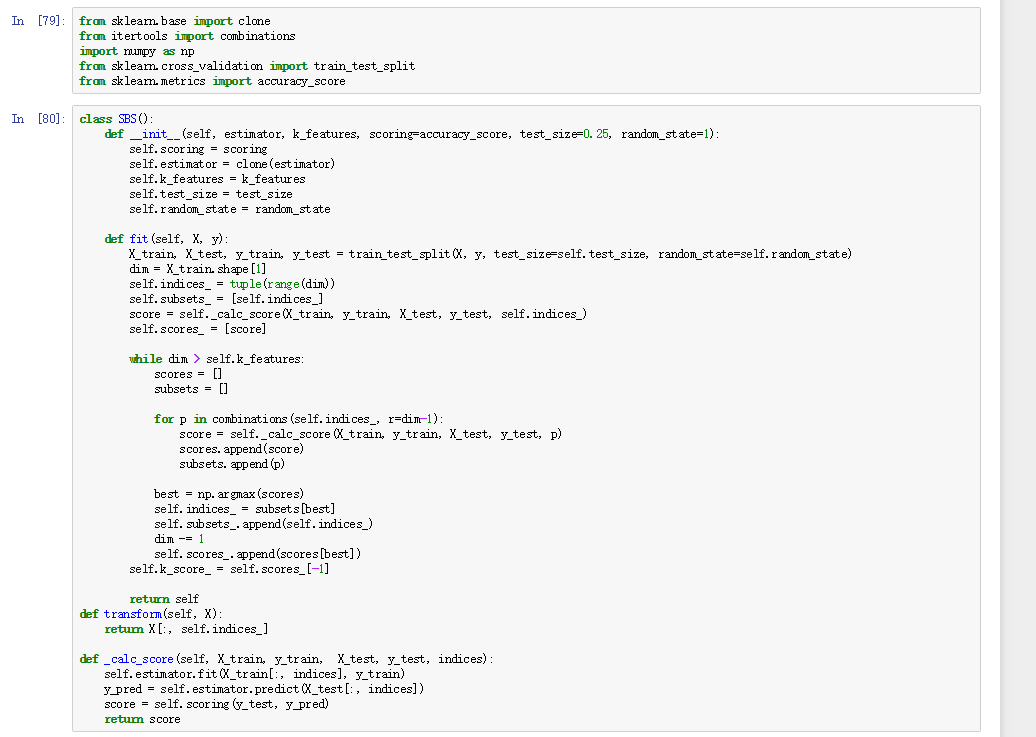
在上面的代码中,我们定义了k_features参数来设定想要得到的特征子集数。使用accuracy_score来评估模型在特征子集的表现。在fit方法的while循环内,通过itertools.combination创建特征子集然后对其评估,
现在我们用KNN作为Estimator来运行SBS算法:
虽然SBS的fit方法中有分割数据集的功能,但我们还是为SBS提供了训练集,然后fit方法将其分割为子训练集和子测试集,而这个子测试集被称为验证集(validation dataset)。
SBS算法记录了每一步最优特征子集的成绩,我们画出每个最优特征子集在验证集上的分类准确率:
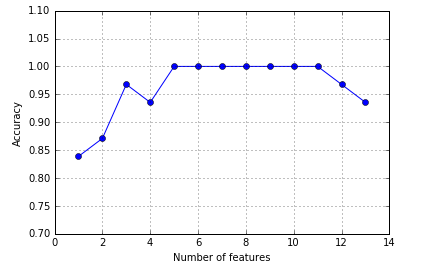
我们可以看到,最开始随着特征数目的减少,分类准确率一直在提高,原因可能是降低了维度诅咒。对于k={5,6,7,8,9,10,11},分类准确率是100%.
我们将最优的5维度特征打印出来看一下:

接下来我们使用整个特征维度来检验KNN模型在测试集的分类准确率:
 、、
、、
可以看到使用原始的特征集建模,在训练集上分类准确率98%,测试集上分类准确率94%,可能是模型有一丢丢过拟合。
我们再使用最优的5维度特征建模看看:

使用不到一半的原始特征,虽然在训练集上分类准确率下降了,但是在测试集上的表现却提高了!并且此时训练集和测试集准确率相差不多,我们很好地降低了过拟合。
Note sklearn中提供了很多特征选择算法。包括基于特征参数的递归后向消除法,基于树方法提供的特征重要性的特征选择法和单变量统计检验。具体的可以看sklearn文档。