PCA进行无监督降维

类似于特征选择，我们可以使用特征抽取来减小数据集中的特征维度。不过，不同于特征选择算法会保留原始特征空间，特征抽取会将原始特征转换/映射到一个新的特征空间。换句话说，特征抽取可以理解为是一种数据压缩的手段，同时保留大部分相关信息(译者注：理解为摘要)。特征抽取是用于提高计算效率的典型手段，另一个好处是也能够减小维度诅咒(curse of dimensionality)，特别是对于没有正则化的模型。

PCA(principal component analysis, 主成分分析)是一种被广泛使用的无监督的线性转换技术，主要用于降维。其他领域的应用还包括探索数据分析和股票交易的信号去噪，基因数据分析和基因表达。

PCA根据特征之间的相关性帮助我们确定数据中存在的模式。简而言之，PCA的目标是找到高维数据中最大方差的方向，并且将高维数据映射到一个新的子空间，这个子空间的方向不大于原始特征空间。新子空间的正交轴(主成分)可以被解释为原始空间的最大方差方向。下图中是原始特征轴，是主成分：

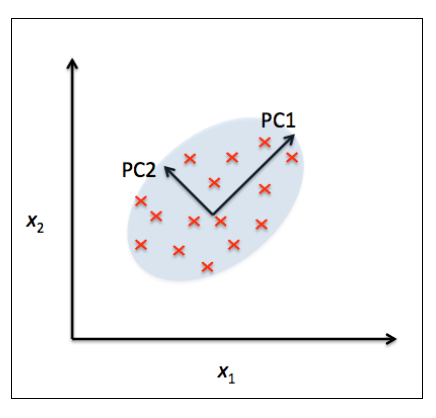
如果使用PCA降维，我们需要构造一个d*k维的转换矩阵，它能将样本向量映射到新的k维度的特征子空间，k<<d:

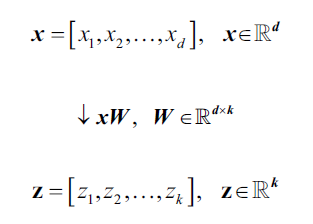
映射后的子空间，第一主成分包含最大的方差，第二主成分包含次大的方差，以此类推，并且各个主成分方向是正交的(不相关)。

PCA方向极其容易受到数据中特征范围影响，所以在运用PCA前一定要做特征标准化，这样才能保证每维度特征的重要性等同。

再详细讲解PCA的细节之前，我们先介绍 PCA的步骤：

• 1 将d维度原始数据标准化。
• 2 构建协方差矩阵。
• 3 求解协方差矩阵的特征向量和特征值。
• 4 选择值最大的k个特征值对应的特征向量，k就是新特征空间的维度，k<<d。
• 5 利用k特征向量构建映射矩阵。
• 6 将原始d维度的数据集X，通过映射矩阵W转换到k维度的特征子空间。