使用松弛变量解决非线性可分的情况
虽然我们不想深挖SVM背后的数学概念,但还是有必要简短介绍一下松弛变量(slack variable) ,它是由Vladimir Vapnik在1995年引入的,借此提出了软间隔分类(soft-margin)。引入松弛变量的动机是原来的线性限制条件在面对非线性可分数据时需要松弛,这样才能保证算法收敛。
松弛变量值为正,添加到线性限制条件即可:
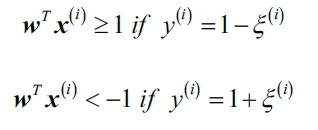
新的目标函数变成了:
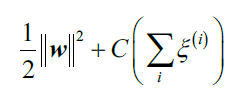
使用变量C,我们可以控制错分类的惩罚量。和逻辑斯蒂回归不同,这里C越大,对于错分类的惩罚越大。可以通过C控制间隔的宽度,在bias-variance之间找到某种平衡:
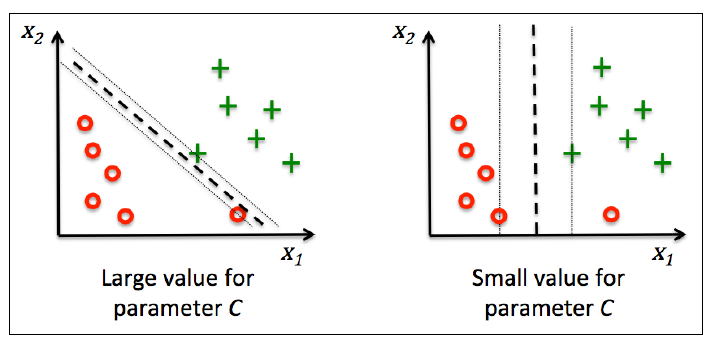
这个概念和正则化相关,如果增大C的值会增加bias而减小模型的方差。
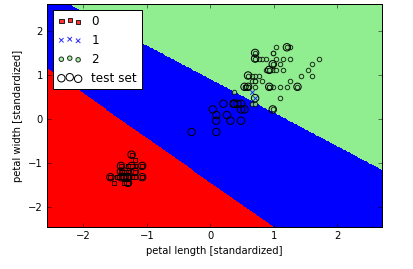
我们已经学会了线性SVM的基本概念,下面使用sklearn训练一个模型:
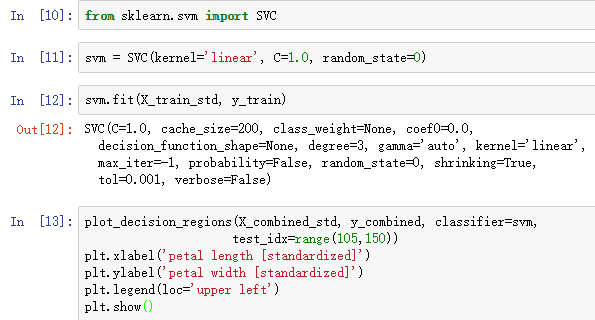
Note 逻辑斯蒂回归 VS SVM
在解决现实的分类问题时,线性逻辑斯蒂回归和线性SVM通常效果近似。逻辑回归目标是最大化训练集的条件似然,使得她更易受奇异值影响。SVM只关心那些离决策界最近的点(即,支持向量)。另一方面,逻辑斯蒂回归的优点是易于实现,特别是并行化实现。此外,面对流式数据,逻辑斯蒂回归的易于更新的特点也很明显。
scikit-learn中不同的实现方式
前面我们用到的sklearn中的Perceptron和LogisticRegression类的实现都使用了LIBLINEAR库,LIBLINEAR是由国立台湾大学开发的一个高度优化过的C/C++库。同样,sklearn中的SVC类利用了国立台湾大学开发的LIBSVM库。
调用LIBLINEAR和LIBSVM而不是用Python自己实现的优点是训练模型速度很快,毕竟是优化过的代码。可是,有时候数据集很大,不能一次读入内存,针对这个问题,sklearn也实现了SGDClassifier类,使用提供的partial_fit方法能够支持在线学习。SGDClassifier利用随机梯度下降算法学习参数。我们可以调用这一个类初始化随机梯度下降版本的感知机、逻辑斯蒂回归和SVM。
