使用核SVM解决非线性

SVM之所以受欢迎度这么高，另一个重要的原因是它很容易核化(kernelized)，能够解决非线性分类问题。在讨论核SVM细节之前，我们先自己创造一个非线性数据集，看看他长什么样子。

使用下面的代码，我们将创造一个简单的数据集，其中100个样本是正类，100个样本是负类。

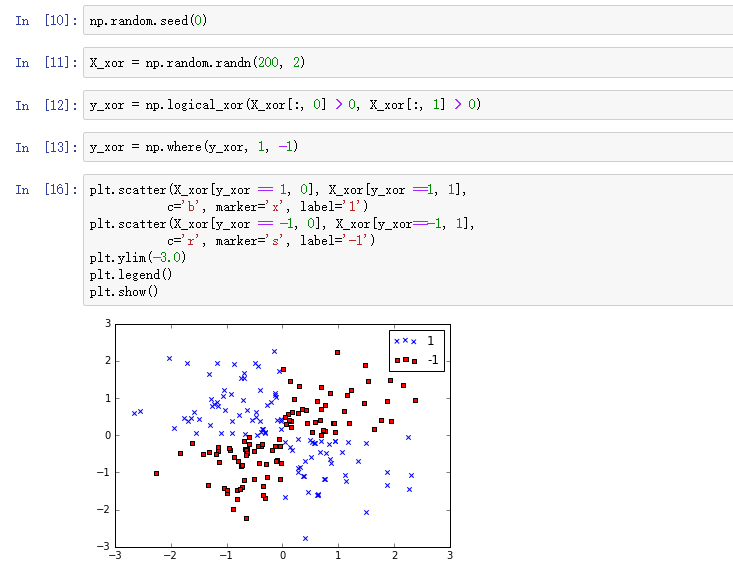
显然，如果要用线性超平面将正负类分开是不可能的，所以前面介绍的线性逻辑斯蒂回归和线性SVM都鞭长莫及。

核方法的idea是为了解决线性不可分数据，在原来特征基础上创造出非线性的组合，然后利用映射函数将现有特征维度映射到更高维的特征空间，并且这个高维度特征空间能够使得原来线性不可分数据变成了线性可分的。

举个例子，下图中，我们将两维的数据映射到三位特征空间，数据集也有线性不可分变成了线性可分，使用的映射为：

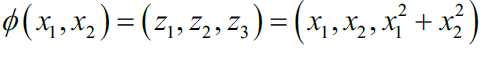
注意看右上角子图到右下角子图的转变，高维空间中的线性决策界实际上是低维空间的非线性决策界，这个非线性决策界是线性分类器找不到的，而核方法找到了：

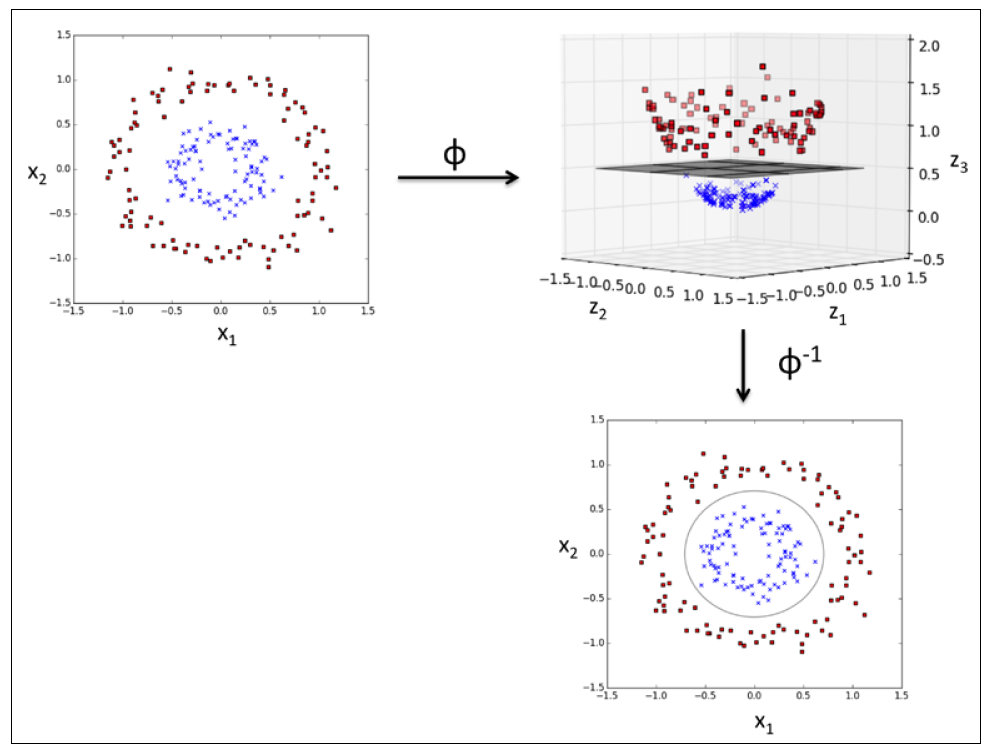
使用核技巧在高维空间找到可分超平面

使用SVM解决非线性问题，我们通过映射函数将训练集映射到高维特征空间，然后训练一个线性SVM模型在新特征空间将数据分类。然后，我们可以使用相同的映射函数对测试集数据分类。

上面的想法很不错，但是如何构建新特征是非常困难的，尤其是数据本身就是高维数据时。因此，我们就要介绍核技巧了。由于我们不会过多涉及在训练SVM时如何求解二次规划问题，你只需要知道用替换就可以了。为了免去两个点的点乘计算， 我们定义所谓的核函数(kernel function):

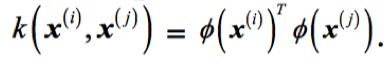
常用的一个核函数是Radial Basis Function kernel(RBF核)，也称为高斯核:

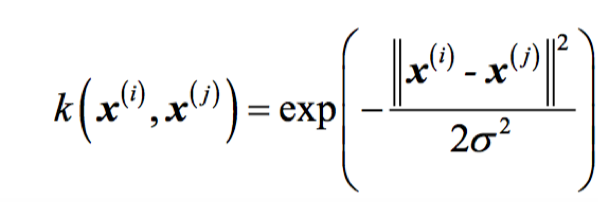
通常简写为：

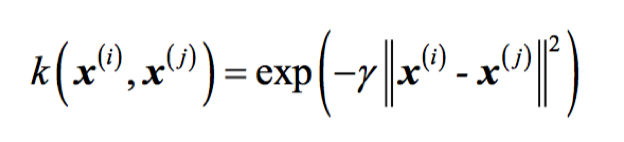
此处，,是一个要优化的自由参数。

通俗地讲，核(kernel)可以被解释为两个样本之间的相似形函数。高斯核中e的指数范围<=0,因此高斯核值域范围,特别地，当两个样本完全一样时，值为1，两个样本完全不同时，值为0.

有了核函数的概念，我们就动手训练一个核SVM，看看是否能够对线性不可分数据集正确分类：

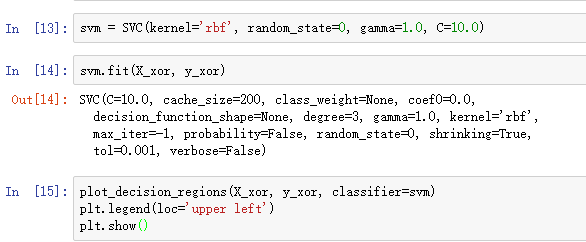
结果如下，可以发现核SVM在XOR数据集上表现相当不错：

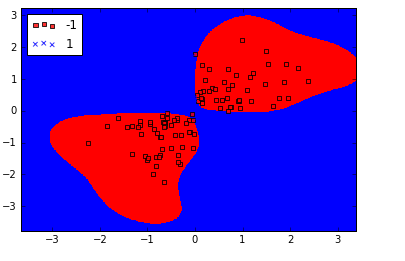
其中参数gamma可以被理解为高斯球面的阶段参数，如果我们增大gamma值，会产生更加柔软的决策界。为了更好地理解gamma参数，我们在Iris数据集上应用RBF核SVM：

我们选择的gamma值相对比较小，所以决策界比较soft：

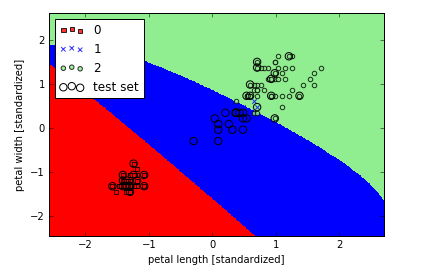
现在我们增大gamma值，然后观察决策界：

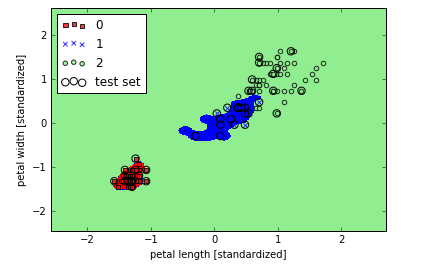
虽然gamma值较大的模型对训练集分类效果很大，但其泛化能力一般很差，所以选择适当的gamma值有助于避免过拟合。

results matching ""

    No results matching ""