k近邻--一个懒惰学习算法

本章我们要讨论的最后一个监督学习算法是k紧邻算法(k-nearest neighbor classifier, KNN), 这个算法很有意思，因为他背后的思想和本章其他算法完全不同。

KNN是懒惰学习的一个典型示例。之所以称为“懒惰”并不是由于此类算法看起来很简单，而是在训练模型过程中这类算法并不去学习一个判别式函数(损失函数)而是要记住整个训练集。

Note 参数模型VS变参模型

机器学习算法可以被分为两大类：参数模型和变参模型。对于参数模型，在训练过程中我们要学习一个函数，重点是估计函数的参数，然后对于新数据集，我们直接用学习到的函数对齐分类。典型的参数模型包括感知机、逻辑斯蒂回归和线性SVM。与之相对的，变参模型中的参数个数不是固定的，它的参数个数随着训练集增大而增多！很多书中变参(nonparametric)被翻译为无参模型，一定要记住，不是没有参数，而是参数个数是变量！变参模型的两个典型示例是决策树/随机森林和核SVM。

KNN属于变参模型的一个子类：基于实例的学习(instance-based learning)。基于实例的学习的模型在训练过程中要做的是记住整个训练集，而懒惰学习是基于实例的学习的特例，在整个学习过程中不涉及损失函数的概念。

KNN算法本身非常简单，步骤如下：

• 1 确定k大小和距离度量。
• 2 对于测试集中的一个样本，找到训练集中和它最近的k个样本。
• 3 将这k个样本的投票结果作为测试样本的类别。

一图胜千言，请看下图：

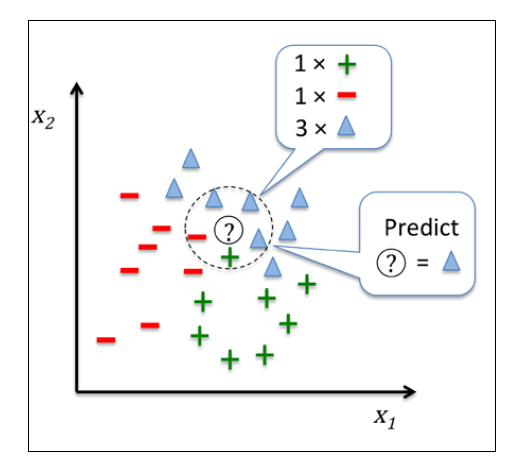
对每一个测试样本，基于事先选择的距离度量，KNN算法在训练集中找到距离最近(最相似)的k个样本，然后将k个样本的类别的投票结果作为测试样本的类别。

像KNN这种基于内存的方法一大优点是：一旦训练集增加了新数据，模型能立刻改变。另一方面，缺点是分类时的最坏计算复杂度随着训练集增大而线性增加，除非特征维度非常低并且算法用诸如KD-树等数据结构实现。此外，我们要一直保存着训练集，不像参数模型训练好模型后，可以丢弃训练集。因此，存储空间也成为了KNN处理大数据的一个瓶颈。

下面我们调用sklearn训练一个KNN模型：

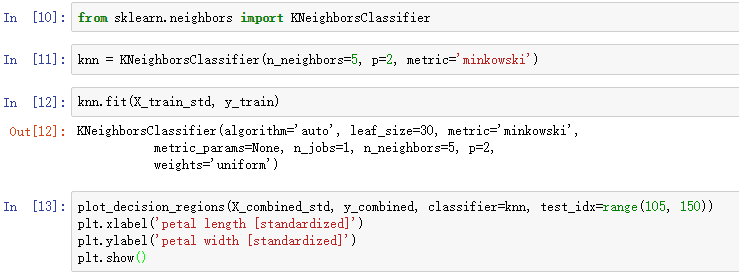
我们设置k=5，得到了相对平滑的决策界：

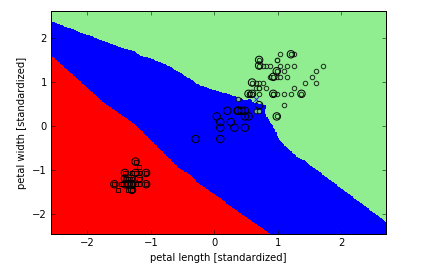
k的选择对于KNN模型来说至关重要，除此之外，距离度量也是很有用的。通常，欧氏距离用于实数域的数据集，此时一定要对特征进行标准化，这样每一维度特征的重要性等同。我们在上面的代码中使用的距离度量是'minkowski',它是欧氏距离和曼哈顿距离的一般化：

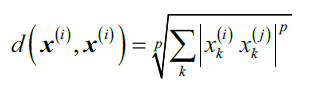
如果p=2，则退化为欧氏距离，p=1，则退化为曼哈顿距离。使用metric参数可以选择不同的距离度量。

Note 维度诅咒

注意，如果特征维度过大，KNN算法很容易过拟合。我们可以想象，对于一个固定大小的训练集，如果特征空间维度非常高，空间中最相似的两个点也可能距离很远(差别很大)。虽然我们在逻辑回归中讨论了正则项来防止过拟合，但是正则项却不适用于KNN和决策树模型，我们只能通过特征选择和降维手段来避免维度诅咒。下一章我们会讲到。