LDA进行监督数据压缩

LDA(linear discriminant analysis, 线性判别分析)是另一种用于特征抽取的技术，它可以提高计算效率，对于非正则模型也能减小过拟合。

虽然LDA的很多概念和PCA很像，但他俩的目标不同，PCA目标是找到正交的主成分同时保持数据集的最大方差，LDA的目标是为每个类单独优化，得到各个类的最优特征子集。PCA和LDA都是线性转换技术，用于数据压缩，前者是无监算法，后者是监督算法。看到监督两个字，可能你会认为对于分类任务，LDA要比PCA效果更好，但实际却不是这样，在某些分类任务情境下，用PCA预处理数据得到的结果要比LDA号，比如，如果每个类含有的样本比较少。

下图画出了对于二分类问题，LDA的一些概念：

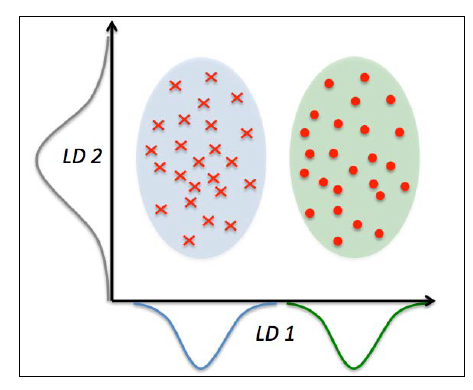
x轴的线性判别(LD 1),很好地将两个正态分布的类别数据分离。虽然y轴的线性判别(LD 2)捕捉了数据集中的大量方差，但却不是一个好的线性判别，因为它没有捕捉任何与类别判别相关的信息。

LDA 的一个假设是数据服从正态分布。同时，我们也假设各个类含有相同的协方差矩阵，每个特征都统计独立。即使真实数据可能不服从上面的某几个假设，但LDA依然具有很好的表现。

在学习LDA内部原理前，我们先将它的几大步骤列出来：

• 1. 将d维度原始数据进行标准化.
• 1. 对每一个类，计算d维度的平均向量.
• 1. 构建类间(between-class)散点矩阵和类内(within-class)散点矩阵.
• 1. 计算矩阵的特征向量和特征值.
• 1. 选择值最大的前k个特征值对应的特征向量，构建d*d维度的转换矩阵,每一个特征向量是的一列.
• 1. 使用矩阵将原始数据集映射到新的特征子空间.

Note 我们在应用LDA时做出的假设是：特征服从正态分布并且彼此独立，每个类的协方差矩阵都相同。现实中的数据当然不可能真的全部服从这些假设，但是不用担心，即使某一个甚至多个假设不成立，LDA也有不俗的表现.(R.O.Duda, P.E. Hart, and D.G.Stork. Pattern Classification. 2nd.Edition. New York, 2001).

计算散点矩阵

数据标准化前面已经说过了，这里就不再讲了，我们说一下如何计算平均向量，然后用这些平均向量分别构建类内散点矩阵和类间散点矩阵。

每一个平均向量存储了类别i的样本的平均特征值:

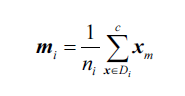
Wine数据集有三个类，每一个的平均向量：

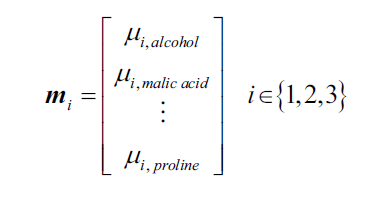
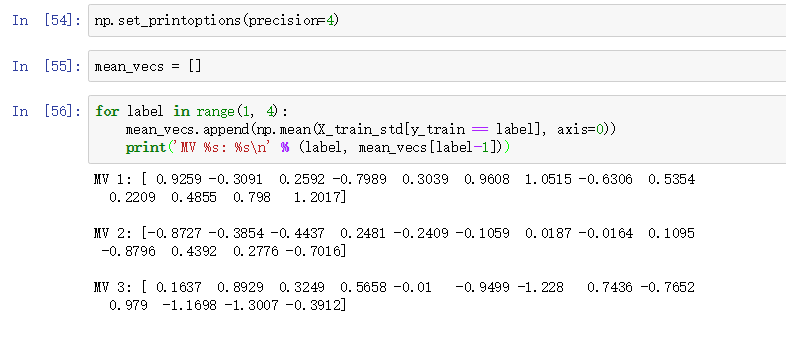
有了平均向量，我们就可以计算类内散点矩阵:

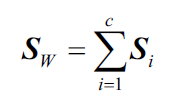
就是每个类的散点矩阵总和。

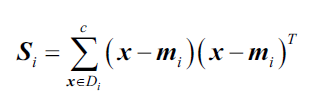
代码：

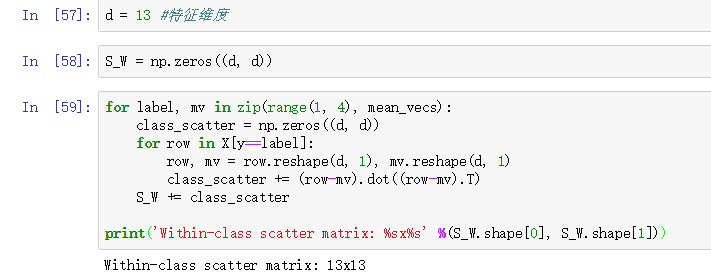
当我们计算散点矩阵时，我们做出的假设是训练集中的类别时均匀分布的。实际情况往往并不是这样，比如我们将Wine训练集各个类别个数打印出来：

所以在得到每个类别的散点矩阵后，我们要将其缩放，然后再相加得到。如果我们将散点矩阵除以各个类别内样本数,我们实际上是在计算协方差矩阵. 协方差矩阵是散点矩阵的归一化结果：

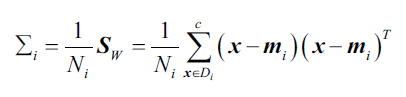
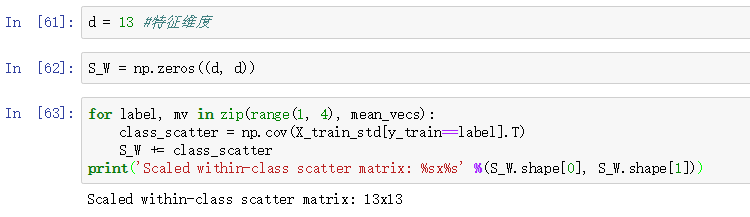
得到缩放后的类内散点矩阵后，我们接下来计算类间散点矩阵:

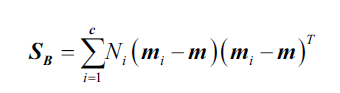
其中，是整个训练集所有样本的特征平均值.

为特征子空间选择线性判别式

剩下的LDA步骤和PCA很像了。不同点是PCA分解协方差矩阵得到特征值和特征向量，LDA分解得到特征值和特征向量：

得到特征值后，对其降序排序：

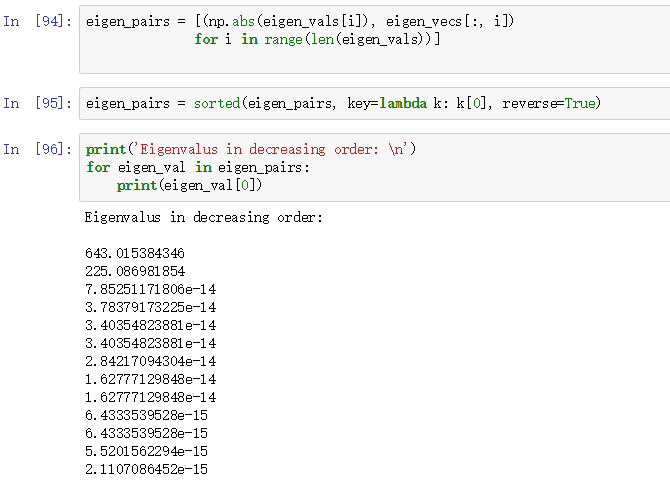
我们可以看到只有两个特征值不为0，其余11个特征值实质是0，这里只不过由于计算机浮点表示才不为0。极端情况是特征向量共线，此时协方差矩阵秩为1，只有一个非0特征值。

为了度量线性判别式(特征向量)捕捉到了多少的类判别信息，我们画出类似方差解释率的线性判别图：

我们可以看到前两个线性判别捕捉到了Wine训练集中100%的有用信息：

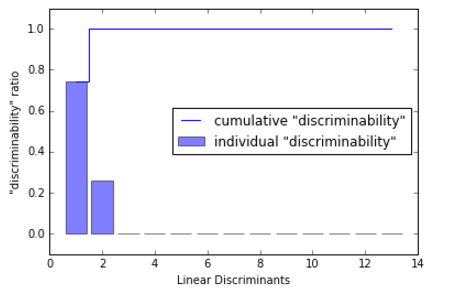
然后由这两个线性判别式来创建转换矩阵: