Python实现自适应线性神经元
既然感知机和Adaline的学习规则非常相似,所以在实现Adaline的时候我们不需要完全重写,而是在感知机代码基础上进行修改得到Adaline,具体地,我们需要修改fit方法,实现梯度下降算法:
class AdalineGD(object):
"""ADAptive LInear NEuron classifier.
Parameters
----------------
eta: float
Learning rate (between 0.0 and 1.0)
n_iter: int
Passes over the training dataset.
Attributes:
------------------
w_: 1d-array
Weights after fitting.
errors_: int
Number of misclassification in every epoch.
"""
def __init__(self, eta=0.01, n_iter=50):
self.eta = eta
self.n_iter = n_iter
def fit(self, X, y):
"""Fit training data.
Parameters
---------------
X: {array-like}, shape=[n_samples, n_features]
Training vectors,
y: array-like, shape=[n_samples]
Target values.
Returns
-----------
self: object
"""
self.w_ = np.zeros(1 + X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
output = self.net_input(X)
errors = (y - output)
self.w_[1:] += self.eta * X.T.dot(errors)
self.w_[0] += self.eta * errors.sum()
cost = (errors ** 2).sum() / 2.0
self.cost_.append(cost)
return self
def net_input(self, X):
""" Calculate net input"""
return np.dot(X, self.w_[1:]) + self.w_[0]
def activation(self, X):
""" Compute linear activation"""
return self.net_input(X)
def predict(self, X):
""" Return class label after unit step"""
return np.where(self.activation(X) >= 0.0, 1, -1)
不像感知机那样每次用一个训练样本来更新权重参数,Adaline基于整个训练集的梯度来更新权重。
注意,X.T.dot(errors)是一个矩阵和向量的乘法,可见numpy做矩阵计算的方便性。
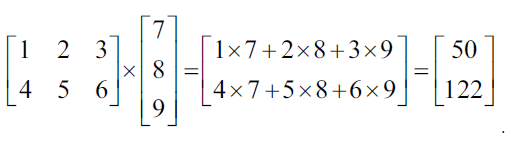
在将Adaline应用到实际问题中时,通常需要先确定一个好的学习率这样才能保证算法真正收敛。我们来做一个试验,设置两个不同的
值:
。然后将每一轮的损失函数值画出来,窥探Adaline是如何学习的.
(学习率,迭代轮数n_iter也被称为超参数(hyperparameters),超参数对于模型至关重要,在第四章我们将学习一些技巧,能够自动找到能使模型达到最好效果的超参数。)
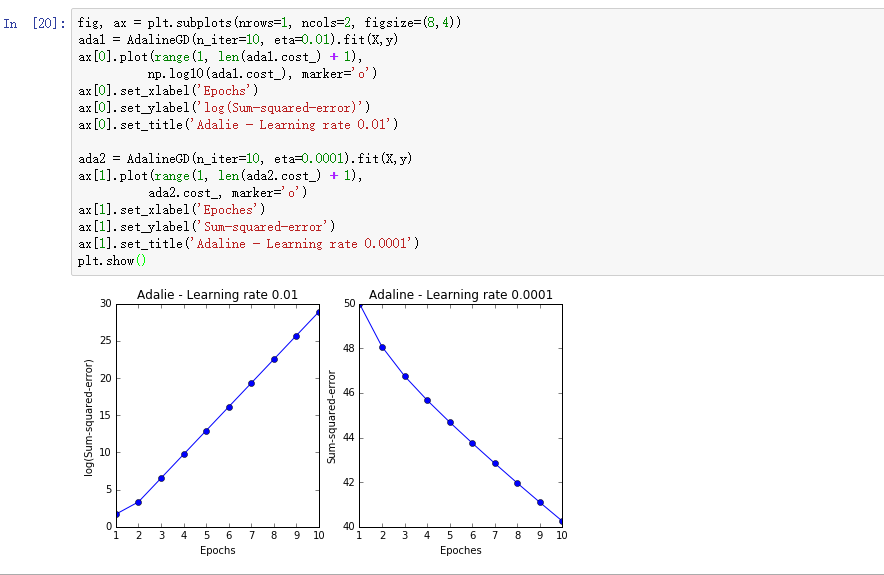
分析上面两幅图各自的问题,左图根本不是在最小化损失函数,反而在每一轮迭代过程中,损失函数值不断在增大!这说明取值过大的学习率不但对算法毫无益处反而危害大大滴。右图虽然能够在每一轮迭代过程中一直在减小损失函数的值,但是减小的幅度太小了,估计至少上百轮迭代才能收敛,而这个时间我们是耗不起的,所以学习率值过小就会导致算法收敛的时间巨长,使得算法根本不能应用于实际问题。
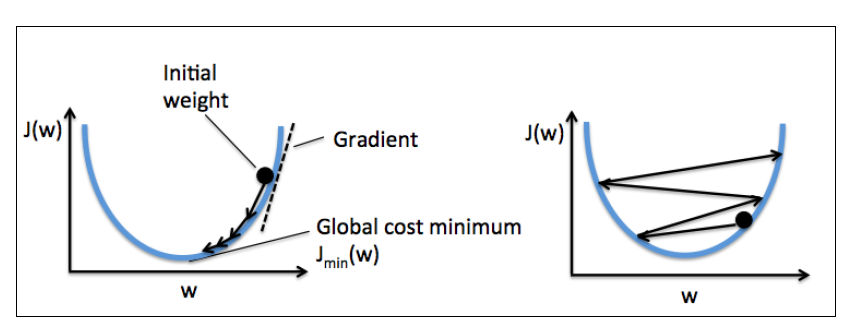
下面左图展示了权重再更新过程中如何得到损失函数最小值的。右图展示了学习率过大时权重更新,每次都跳过了最小损失函数对应的权重值。
许多机器学习算法都要求先对特征进行某种缩放操作,比如标准化(standardization)和归一化(normalization)。而缩放后的特征通常更有助于算法收敛,实际上,对特征缩放后在运用梯度下降算法往往会有更好的学习效果。
特征标准化的计算很简单,比如要对第j维度特征进行标准化,只需要计算所有训练集样本中第j维度的平均值和标准差
即可,然后套公式:
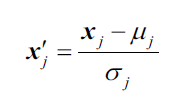
标准化后的特征 均值为0,标准差为1.
在Numpy中,调用mean和std方法很容易对特征进行标准化:

标准化后,我们用Adaline算法来训练模型,看看如何收敛的(学习率为0.01):

我们将决策界和算法学习情况可视化出来:
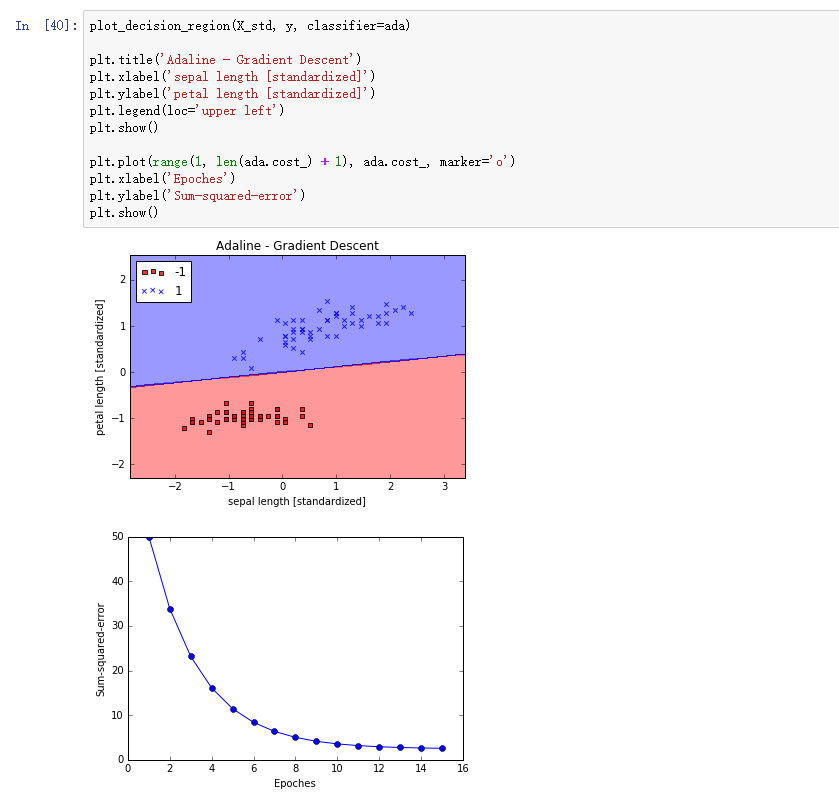
Wow 标准化后的数据再使用梯度下降Adaline算法竟然收敛了! 注意看Sum-squared-error(即,)最后并没有等于0,即使所有样本都正确分类。