聊一聊方差

本节，我们会学习PCA中的前四个步骤：标准化数据、构建协方差矩阵、得到特征值和特征向量以及对特征值排序得到排名靠前的特征向量。

数据集还是用第四章介绍过的Wine数据集，先将原始Wine分割为训练集和测试集，然后标准化：

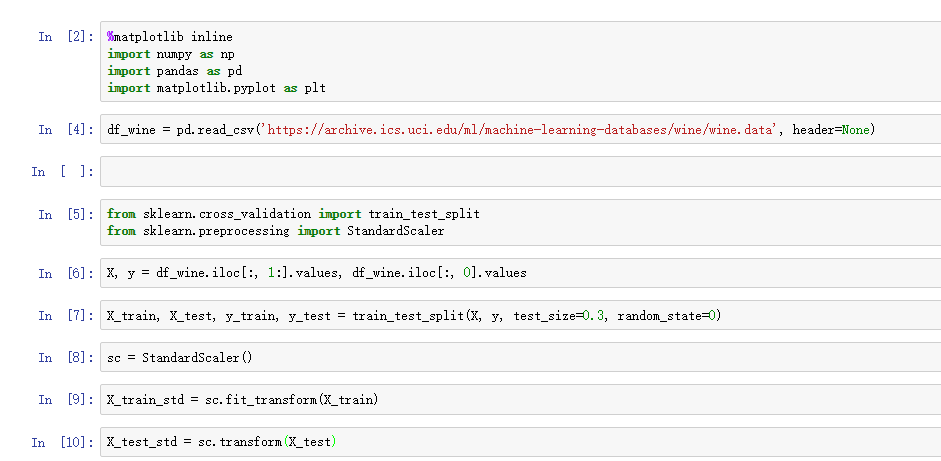
上面的代码完成了PCA的第一步，对数据进行标准化。我们再来看第二步：构建协方差矩阵。协方差矩阵是对称矩阵，d*d维度，其中d是原始数据的特征维度，协方差矩阵的每个元素是两两特征之间的协方差。

举个例子，特征的协方差计算公式如下：

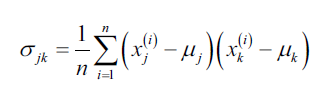
其中，分别是样本中第j维度特征和第k维度特征的平均值。由于我们已经将数据标准化了，所以这里。 如果意味着j和k这两维度特征值要么同时增加要么同时衰减，反之,意味着这两个特征的值变化方向相反。

假设数据有三维度特征，协方差矩阵如下：

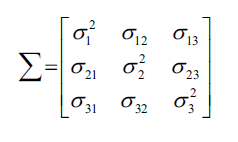
协方差矩阵的特征向量代表了主成分(最大方差的方向)，对应的特征值决定了特征向量绝对值的大小。在Wine数据集对应的13*13的协方差矩阵，我们会得到13个特征值。

如何得到特征值和特征向量呢？会议线性代数课上讲过的内容：

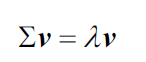
其中，。我们当然不可能手算特征值，NumPy提供了linalg.eig函数用于得到特征值和特征向量：

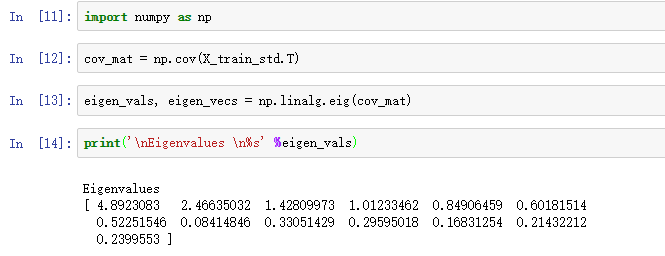
我们先使用np.cov方法得到数据的协方差矩阵，然后利用linalg.eig方法计算出特征向量(eigen_vecs)和特征值(eigen_vals)。

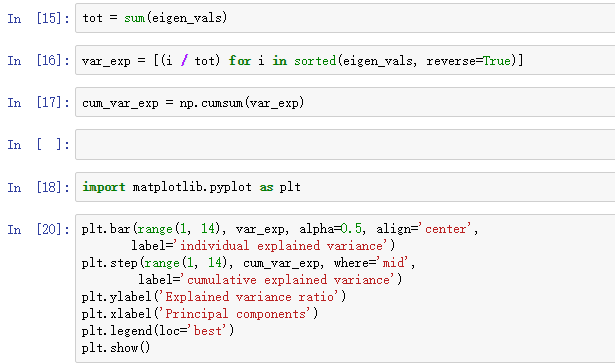
由于我们的目的是数据压缩，即降维，所以我们只将那些包含最多信息(方差)的特征向量(主成分)拿出来。什么样的特征向量包含的信息最多呢？这就要看特征值了，因为特征值定义了特征向量的大小，我们先对特征值进行降序排序，前k个特征值对应的特征向量就是我们要找的主成分。

我们再学一个概念：方差解释率(variance explained ration)。一个特征值的方差解释率就是次特征值在特征值总和的占比：

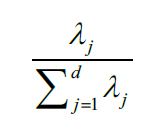
利用NumPy提供的cumsum函数，我们可以计算累计解释方差和：

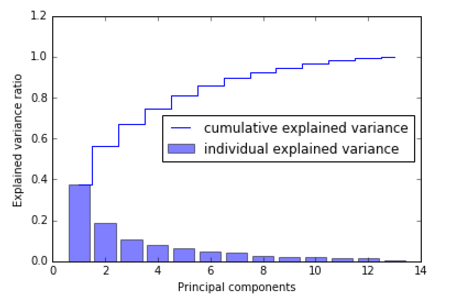
从上面的结果图我们可以看到第一个主成分占了近40%的方差(信息)，前两个主成分占了60%的方差。

很多同学看到这里，可能将方差解释率和第四章讲到的用随机森林评估特征重要性联系起来，二者还是有很大区别的，PCA是一种无监督方法，在整个计算过程中我们都没有用到类别信息！随机森林是监督模型，建模时用到了类别信息。

方差的物理含义是对值沿着特征轴的传播进行度量。