映射新的数据点

在前面的两个例子中，我们将原始的数据集映射到新的特征空间。不过在实际应用中，我们常常需要将多个数据集转换，比如训练集和测试集，还有可能在训练好模型后，又收集到的新数据。在本节，你将学习如何将不属于训练集的数据进行映射。

还记得在标准PCA中，我们通过计算 转换矩阵*输入样本，得到映射后的数据。转换矩阵的每一列是我们从协方差矩阵中得到的k个特征向量。现在，如何将这种思路应用到核PCA？在核PCA中，我们得到的特征向量来自归一化的核矩阵(centered kernel matrix)，而不是协方差矩阵，这意味着样本已经被映射到主成分轴.因此，如果我们要把一个新样本 映射到主成分轴，我们要按照下式:

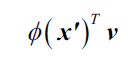
上式怎么算？当然不好算，好在我们还有核技巧，所以可以避免直接计算。

和标准PCA不同的是，核PCA是一种基于内存的方法，这是什么意思呢？意思是每次对新样本进行映射时就要用到所有的训练集。因为要计算训练集中每个样本和新样本之间的RBF核(相似度):

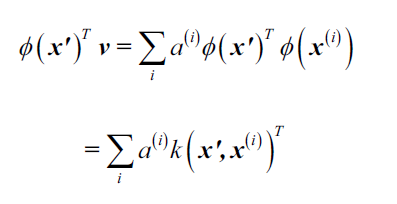
其中，核矩阵的特征向量和特征值满足条件: 。

计算每一个训练集样本和新样本的后，我们必须用特征值对特征向量做归一化。所以呢，我们要修改一下前面实现的RBF PCA，能够返回核矩阵的特征向量：

from scipy.spatial.distance import pdist, squareform
from scipy import exp
from scipy.linalg import eigh
import numpy as np

def rbf_kernel_pca(X, gamma, n_components):
    """
    RBF kernel PCA implementation.
    """
    # Calculate pairwise squared Eculidean distances
    sq_dists = pdist(X, 'sqeuclidean')

    mat_sq_dists = squareform(sq_dists)
    #Compute the symmetric kernel matrix
    K = exp(-gamma * mat_sq_dists)
    #Center the kernle matrix
    N = K.shape[0]
    one_n = np.ones((N, N)) / N
    K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)

    #Obtaining eigenpairs from the centered kernel matrix
    eigvals, eigvecs = eigh(K)

    alphas = np.column_stack((eigvecs[:, -i]
                             for i in range(1,n_components+1)))

    #Collect the corresponding eigenvalues
    lambdas = [eigvals[-i] for i in range(1, n_components+1)]

    return alphas, lambdas

现在，我们创建一个新的半月形数据集，然后用更新过的核PCA将其映射到一维子空间：

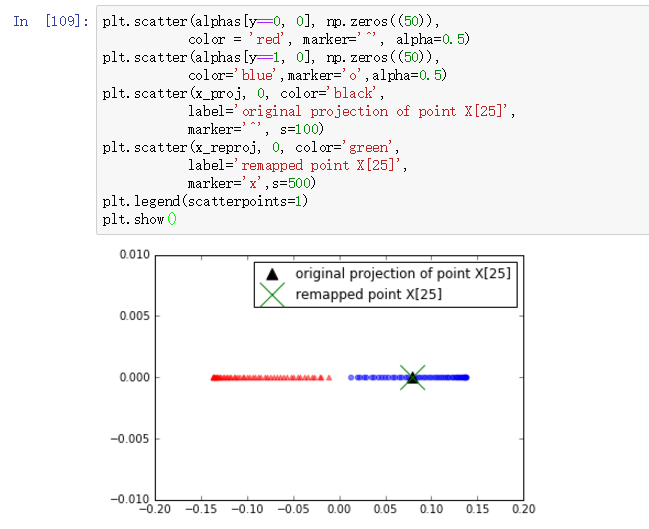
为了检验对于新数据点的映射表现，我们假设第26个点时新数据点，我们的目标就是将这个新数据点进行映射:

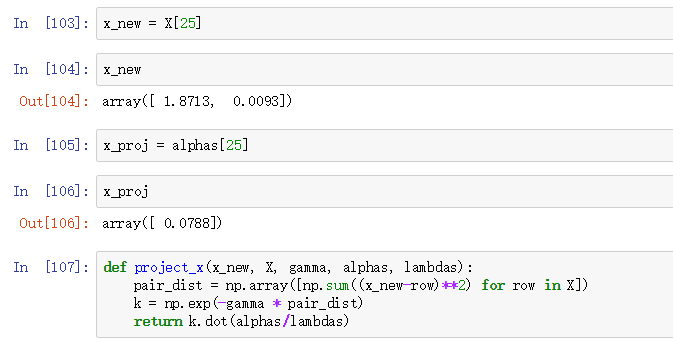
使用project_x函数，我们能够对新数据样本进行映射：

最后，我们将第一主成分进行可视化：