特征转换

在得到特征向量后，接下来我们就可以对原始特征进行转换了。本节我们先对特征值进行降序排序，然后用特征向量构建映射矩阵，最后用映射矩阵将原始数据映射到低维度特征子空间。

先对特征值排序：

接下来，我们选择最大的两个特征值对应的特征向量，这里只用两个特征向量是为了下面画图方便，在实际运用PCA时，到底选择几个特征向量，要考虑到计算效率和分类器的表现两个方面(译者注：常用的选择方式是特征值子集要包含90%方差)：

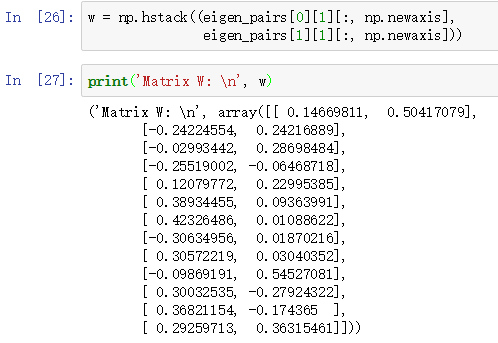
现在，我们创建了一个132的的映射矩阵W。然后对样本(113维度)进行映射，就能得到2维度的新样本：

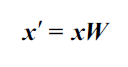
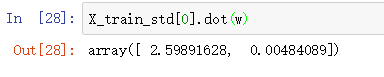
直接对原始数据(124*13)映射：

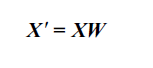
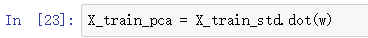
特征维度降到2维度后，我们就可以用散点图将数据可视化出来了：

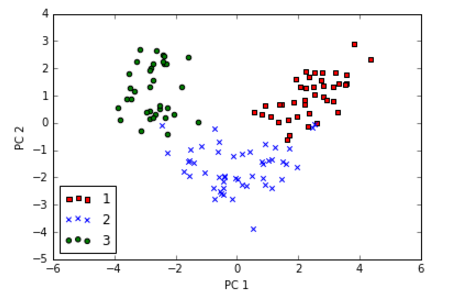
从上图可以看到，数据在x轴(第一主成分)上要比y轴(第二主成分)分布更广，这也符合方差解释率的结果。数据降维后，直觉上使用线性分类器就能够将数据分类。

scikit-learn中的PCA

上一小节我们详细讨论了PCA的步骤，在实际应用时，一般不会使用自己实现，而是直接调用sklearn中的PCA类，PCA类是另一个transformer类：我们先用训练集训练模型参数，然后统一应用于训练集和测试集。

下面我们就是用sklearn中的PCA类对Wine数据降维，然后调用逻辑斯蒂回归模型分类，最后将决策界可视化出来：

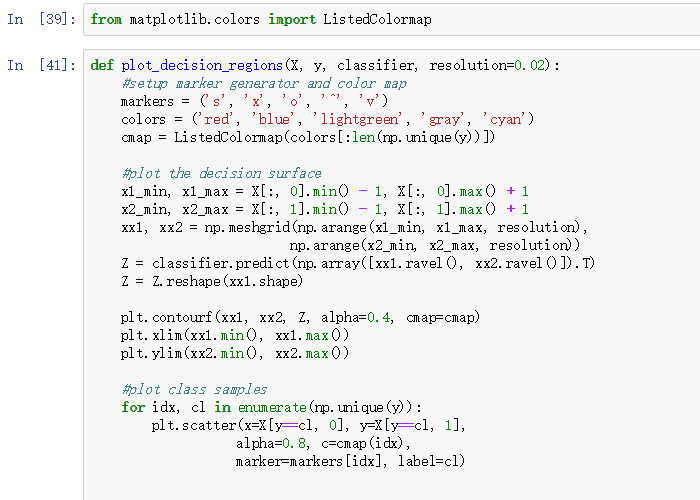
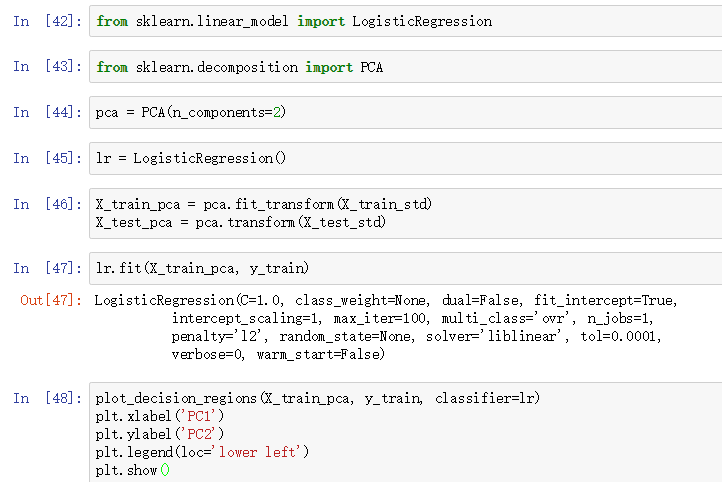
执行上面的代码，我们应该得到如下的决策界：

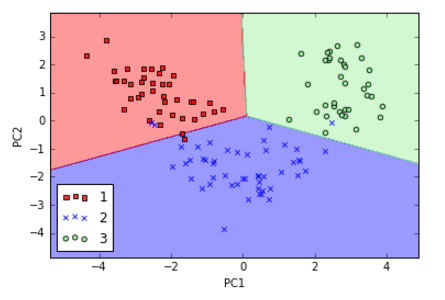
如果你仔细观察我们自己实现的PCA得到的散点图和调用sklearn中PCA得到的散点图，两幅图看起来是镜像关系！这是由于NumPy和sklearn求解特征向量时计算的差异，如果你实在看不惯，只需要将其中一个得到的特征向量*(-1)即可。还要注意特征向量一般都要归一化。

我们再看看决策界在测试集的分类效果：

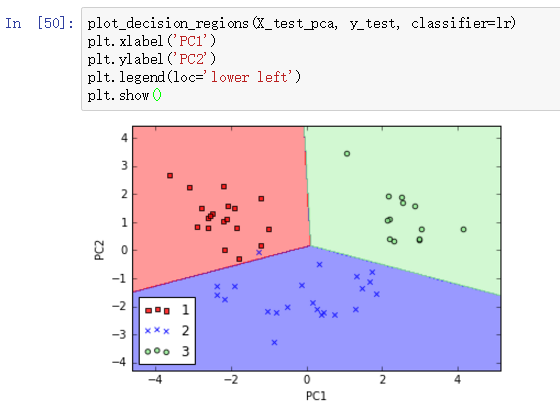
啊哈！测试集仅有一个样本被错误分类，效果很棒。

怎样用sklearn的PCA得到每个主成分(不是特征)的方差解释率呢？很简单，初始化PCA时，ncomponents设置为None，然后通过explained_variance_ratio属性得到每个主成分的方差解释率：

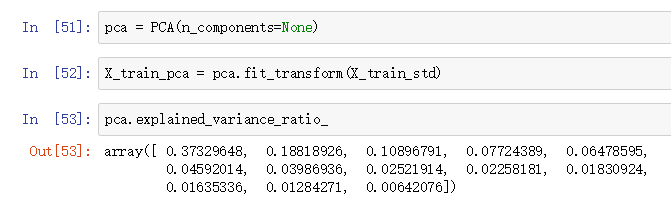
此时n_components=None, 我们并没有做降维。