用Python实现核PCA

上一节我们讨论了核PCA的原理。现在我们根据上一节的三个步骤，自己实现一个核PCA。借助SciPy和NumPy，其实实现核PCA很简单：

RBF核PCA的一个缺点是需要人工设置值，调参不易。第六章我们会介绍调参技巧。

例1 半月形数据分割

现在我们创建一个非线性数据集试一下rbf_kernel_pca的效果，数据集100个样本，每个样本两维度特征，数据分布呈两个半月形：

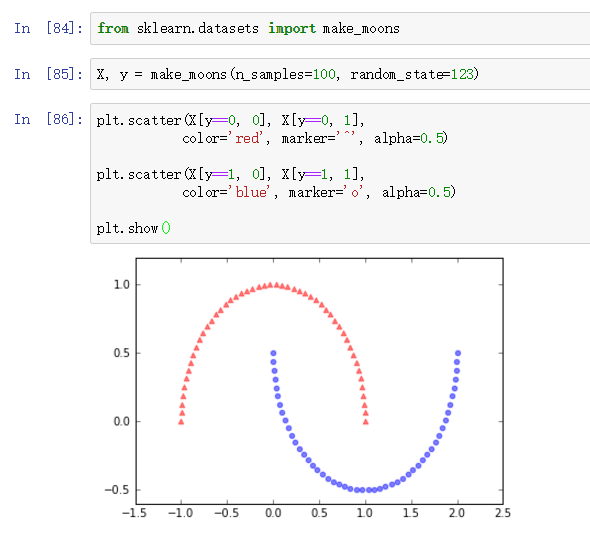
每个半月数据是一类。

显然图中的数据不是线性可分的，我们的目标是通过核PCA将"曲线"映射到"直线"上，然后就可以用线性分类器了。

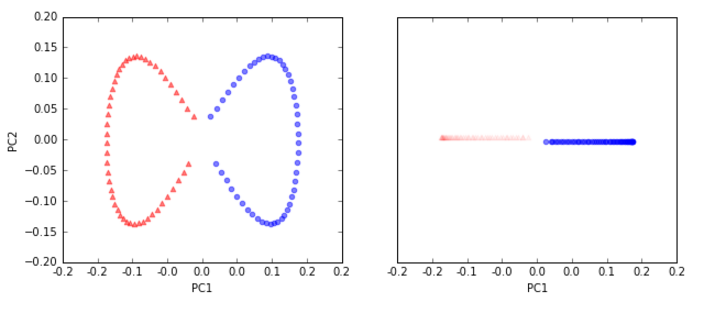
我们先看一下如果用标准PCA处理，会得到什么结果：

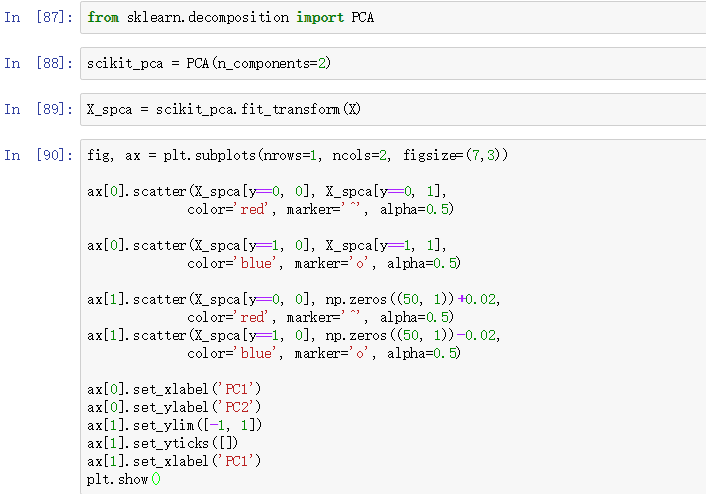
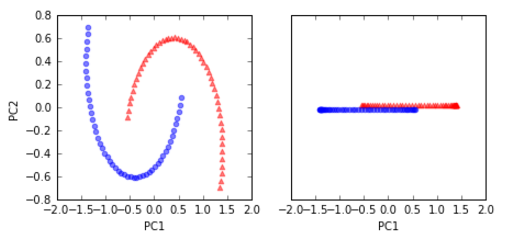
很显然，用标准PCA降维后的数据无法用线性分类器处理。还要注意右边子图中的蓝线我们故意下调了一点点，红线上调了一点点，这是为了清楚地观察他们的重合部分。

现在我们尝试rbf_kernel_pca，看看能不能解决非线性数据：

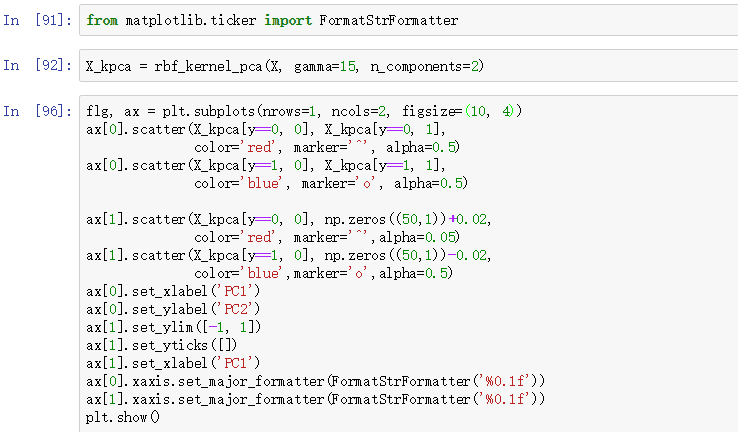
我们可以看到经过核PCA处理后的数据线性可分了，所以可以直接用线性分类器来训练一个合适的模型。

RBF核PCA的缺点就是需要人工设定，这个值不是凭空瞎想的，而是要做实验确定，在第六章，我们会讨论调参的技巧。

例2 分离同心圆数据

上一节我们创建了一个半圆形的数据，然后可以用核PCA线性分离，我们再来看另一个有趣的非线性数据集：

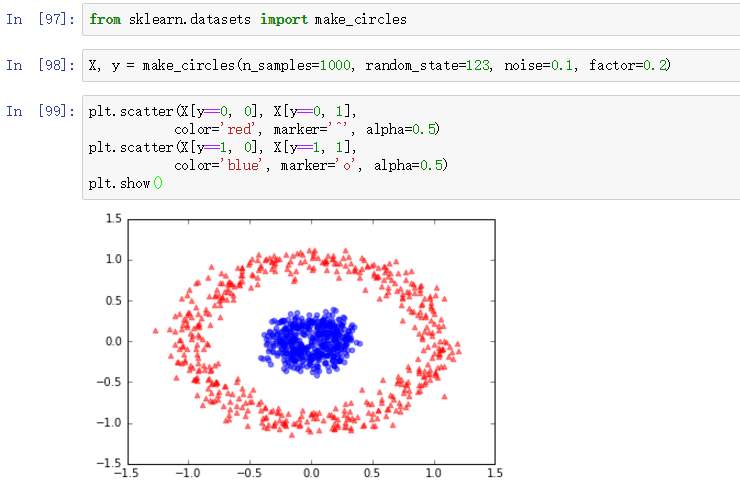
同样这也是一个二分类问题。我们分别用标准PCA和RBF核PCA处理数据集，然后比较他们的结果：

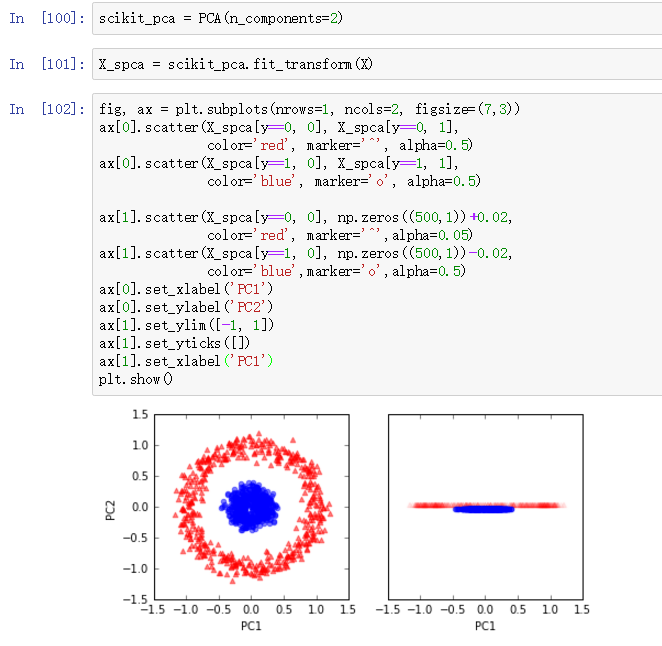
标准PCA效果不好，处理后不能应用线性分类器。

再来看看RBF核PCA的效果能不能让我们满意：

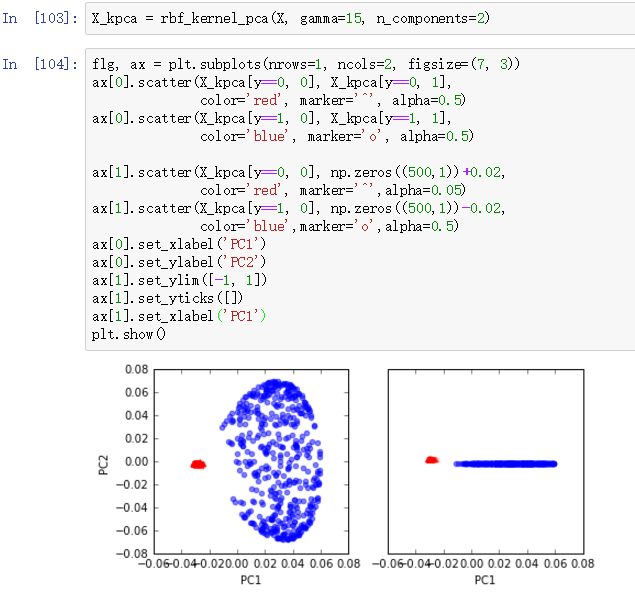
Wow，结果非常好。