大规模机器学习和随机梯度下降
在上一节我们学习了如何使用梯度下降法最小化损失函数,由于梯度下降要用到所有的训练样本,因此也被称为批梯度下降(batch gradient descent)。现在想象一下我们有一个非常大的数据集,里面有几百万条样本,现在用梯度下降法来训练模型,可以想象计算量将是非常大,每一次求梯度都要用到所有的样本。能不能用少量的样本来求梯度呢?
随机梯度下降法(stochastic gradient descent)诞生啦!有时也被称为迭代(iteration)/在线(on-line)梯度下降。随机梯度下降法每次只用一个样本对权重进行更新(译者注:唔,感知机算法也如此,转了一圈,历史又回到了起点。):
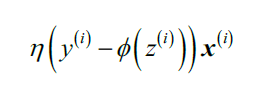
虽然随机梯度下降被当作是梯度下降的近似算法,但实际上她往往比梯度下降收敛更快,因为相同时间内她对权重更新的更频繁。由于单个样本得到的损失函数相对于用整个训练集得到的损失函数具有随机性,反而会有助于随机梯度下降算法避免陷入局部最小点。在实际应用随机梯度下降法时,为了得到准确结果,一定要以随机方式选择样本计算梯度,通常的做法在每一轮迭代后将训练集进行打乱重排(shuffle)。
Notes:在随机梯度下降法中,通常用不断减小的自适应学习率替代固定学习率,比如
,其中
是常数。还要注意随机梯度下降并不能够保证使损失函数达到全局最小点,但结果会很接近全局最小。
随机梯度下降法的另一个优点是可以用于在线学习(online learning)。在线学习在解决不断累积的大规模数据时非常有用,比如,移动端的顾客数据。使用在线学习,系统可以实时更新并且如果存储空间快装不下数据了,可以将时间最久的数据删除。
Notes 除了梯度下降算法和随机梯度下降算法之外,还有一种常用的二者折中的算法:最小批学习(mini-batch learning)。很好理解,梯度下降每一次用全部训练集计算梯度更新权重,随机梯度法每一次用一个训练样本计算梯度更新权重,最小批学习每次用部分训练样本计算梯度更新权重,比如50。相对于梯度下降,最小批收敛速度也更快因为权重参数更新更加频繁。此外,最小批相对于随机梯度中,使用向量操作替代for循环(每一次跌倒都要遍历所有样本),使得计算更快。
上一节我们已经实现了梯度下降求解Adaline,只需要做部分修改就能得到随机梯度下降法求解Adaline。第一个修改是fit方法内用每一个训练样本更新权重参数,第二个修改是增加partial_fit方法,第三个修改是增加shuffle方法打乱训练集顺序。
from numpy.random import seed
class AdalineSGD(object):
"""ADAptive LInear NEuron classifier.
Parameters
---------------
eta: float
Learning rate (between 0.0 and 1.0)
n_iter: int
Passes over the training dataset.
Attributes
---------------
w_: 1d-array
Weights after fitting.
errors_: list
Number of misclassification in every epoch.
shuffle: bool (default: True)
Shuffles training data every epoch
if True to prevent cycles.
random_state: int (default: None)
Set random state for shuffling
and initializing the weights.
"""
def __init__(self, eta=0.01, n_iter=10, shuffle=True, random_state=None):
self.eta = eta
self.n_iter = n_iter
self.w_initialized = False
self.shuffle = shuffle
if random_state:
seed(random_state)
def fit(self, X, y):
"""Fit training data.
Parameters
-----------
X: {array-like}, shape=[n_samples, n_features]
y: array-like, shape=[n_samples]
Returns
--------------
self: object
"""
self._initialize_weights(X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
if self.shuffle:
X, y = self._shuffle(X, y)
cost = []
for xi, target in zip(X, y):
cost.append(self._update_weights(xi, target))
avg_cost = sum(cost)/len(y)
self.cost_.append(avg_cost)
return self
def partial_fit(self, X, y):
"""Fit training data without reinitializing the weights."""
if not self.w_initialized:
self._initialize_weights(X.shape[1])
if y.ravel().shape[0] > 1:
for xi, target in zip(X, y):
self._update_weights(xi, target)
else:
self._update_weights(X, y)
return self
def _shuffle(self, X, y):
"""Shuffle training data"""
r = np.random.permutation(len(y))
return X[r], y[r]
def _initialize_weights(self, m):
"""Initialize weights to zeros"""
self.w_ = np.zeros(1 + m)
self.w_initialized = True
def _update_weights(self, xi, target):
"""Apply Adaline learning rule to update the weights"""
output = self.net_input(xi)
error = (target - output)
self.w_[1:] += self.eta * xi.dot(error)
self.w_[0] += self.eta * error
cost = 0.5 * error ** 2
return cost
def net_input(self, X):
"""Calculate net input"""
return np.dot(X, self.w_[1:]) + self.w_[0]
def activation(self, X):
"""Compute linear activation"""
return self.net_input(X)
def predict(self, X):
"""Return class label after unit step"""
return np.where(self.activation(X) >= 0.0, 1, -1)
_shuffle方法的工作方式:调用numpy.random中的permutation函数得到0-100的一个随机序列,然后这个徐列作为特征矩阵和类别向量的下标,就起到了shuffle的功能。
我们使用fit方法训练AdalineSGD模型,使用plot_decision_regions对训练结果画图:

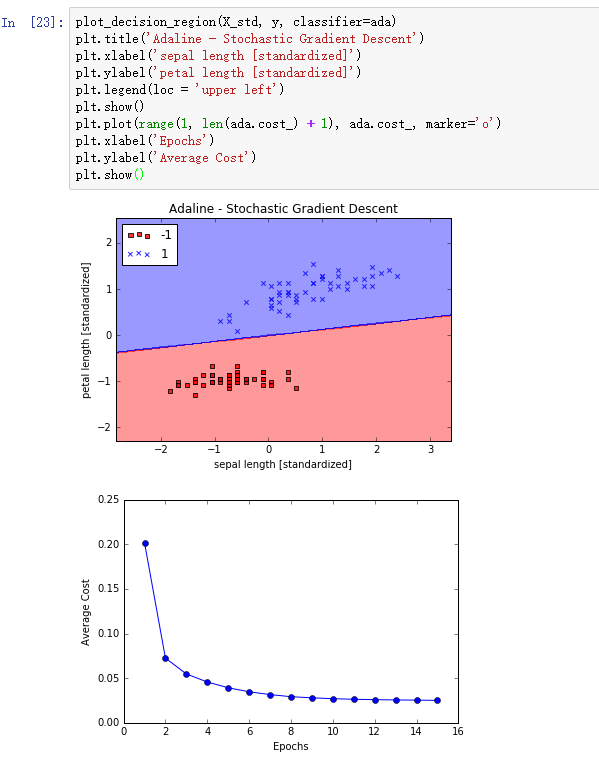
我们可以发现,平均损失(average cost)下降的非常快,在第15次迭代后决策界和使用梯度下降的Adaline决策界非常相似。如果我们要在在线环境下更新模型参数,通过调用partial_fit方法即可,此时参数是一个训练样本,比如ada.partial_fit(X_std[0, :], y[0])。