scikit-learn之旅

在第二章，你学习了两个分类相关的算法：感知机和Adaline，并且都用Python进行了实现。现在我们学习scikit-learn的API，这个库不但用户界面友好并且对常用算法的实现进行了高度优化。此外，它还包含数据预处理和调参和模型评估的很多方法，是Python进行数据挖掘的必备工具。

通过scikit-learn训练感知机模型

我们先看一下如何使用sklearn训练一个感知机模型，数据集还是用我们熟悉的Iris数据集。由于sklearn已经内置了Iris数据集，所以本章所有的分类算法我们通通使用Iris数据集，还是和第二章一样，为了可视化方便，我们只使用其中两维度特征，样本数则使用三个类别全部的150个样本。

为了评估训练好的模型对新数据的预测能力，我们先把Iris训练集分割为两部分：训练集和测试集。在第5章我们还会讨论模型评估的更多细节。

通过调用train_tset_split方法我们将数据集随机分为两部分，测试集占30%(45个样本)，训练集占70%(105个样本)。

许多机器学习和优化算法都要求对特征进行缩放操作，回忆第二章中梯度下降的例子，当时我们自己实现了标准化代码，现在我们可以直接调用sklearn中的StandardScaler来对特征进行标准化：

上面的代码中我们先从preprocessing模块中读取StandardScaler类，然后得到一个初始化的StandardScaler新对象sc，使用fit方法，StandardScaler对训练集中每一维度特征计算出(样本平均值)和(标准差)，然后调用transform方法对数据集进行标准化。注意我们用相同的标准化参数对待训练集和测试集。

对数据标准化以后，我们可以训练一个感知机模型。sklearn中大多数算法都支持多类别分类，默认使用One-vs.-Rest方式实现。所以我们可以直接训练三分类的感知机模型:

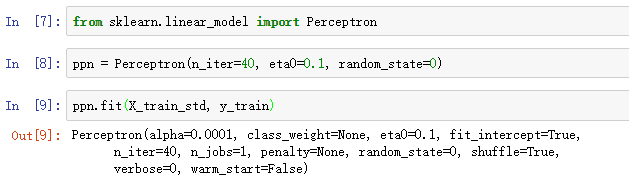
sklearn中训练模型的接口和我们在第二章实现的一样耶，从linear_model模型读取Perceptron类，然后初始化得到ppn，接着使用fit方法训练一个模型。这里的eta0就是第二章中的学习率eta，n_iter同样表示对训练集迭代的次数。我们设置random_state参数使得shuffle结果可再现。

训练好感知机模型后，我们可以使用predict方法进行预测了：

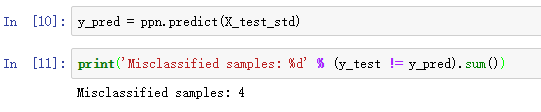
对于测试集中45个样本，有4个样本被错分类了，因此，错分类率是0.089。除了使用错分类率，我们也可以使用分类准确率(accuracy)评价模型，accuracy=1-miscassification error = 1-0.089=0.911。

Sklearn中包含了许多评价指标，这些指标都位于metrics模块，比如，我们可以计算分类准确率:

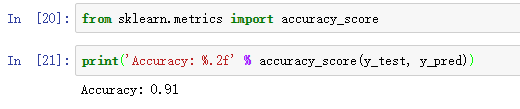
Notes 本章我们评估模型性能的好坏仅仅依赖于其在测试集的表现。在第5章，你将会学习许多其他的技巧来评估模型，包括可视化分析来检测和预防过拟合(overfitting)。过拟合意味着模型对训练集中的模式捕捉的很好，但是其泛化能力却很差。

最后，我们使用第二章的plot_decision_regions画出分界区域。不过在使用之间，我们进行一点小修改，我们用圆圈表示测试集样本：

from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt

def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):
    # setup marker generator and color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])

    # plot the decision surface
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
                            np.arange(x2_min, x2_max, resolution))
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)
    plt.contourf(xx1, xx2, Z, slpha=0.4, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())

    # plot all samples
    X_test, y_test = X[test_idx, :], y[test_idx]
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],
                    alpha=0.8, c=cmap(idx),
                    marker=markers[idx], label=cl)

    # highlight test samples
    if test_idx:
        X_test, y_test = X[test_idx, :], y[test_idx]
        plt.scatter(X_test[:, 0], X_test[:, 1], c='',
                    alpha=1.0, linewidth=1, marker='o',
                    s=55, label='test set')

经过上面的修改，现在可以区分训练集和测试集，运行如下代码：

对结果可视化后，我们可以发现三个类别的花不能被线性决策界完美分类：

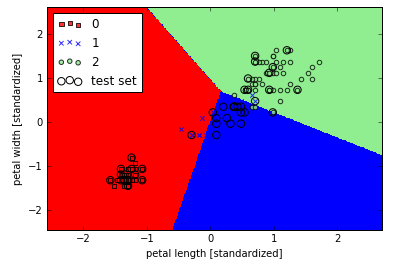
在第二章我们就说过，感知机对于不能够线性可分的数据，算法永远不会收敛，这也是为什么我们不推荐大家实际使用感知机的原因。在接下来的章节，我们将学习到其他线性分类器，即使数据不能完美线性分类，也能收敛到最小的损失值。