统一特征取值范围

特征缩放(feature scaling)是预处理阶段的关键步骤，但常常被遗忘。虽然存在决策树和随机森林这种是少数不需要特征缩放的机器学习算法，但对于大部分机器学习算法和优化算法来说，如果特征都在同一范围内，会获得更好的结果。比如第二章提到的梯度下降法。

特征缩放的重要性可以通过一个简单的示例解释。假设我们有两个特征，一个特征的取值范围是[1,10],另一个特征的取值范围是[1,100000]。我们使用Adaline中的平方误差函数，很明显，权重更新时会主要根据第二维度特征，这就使得在权重更新过程中第一个特征的话语权很小。另一个例子是如果kNN算法用欧氏距离作为距离度量，第二维度特征也占据了主要的话语权。

有两种方法能使不同的特征有相同的取值范围：归一化(normalization)和标准化(standardization)。两种方法还是有必要区分一下的。归一化指的是将特征范围缩放到[0,1]，是最小-最大缩放(min-max scaling)的特例。为了得到归一化结果，我们对每一个特征应用最小-最大缩放，计算公式如下：

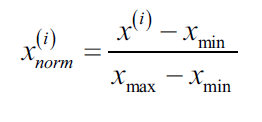
其中，是归一化后的结果，是对应的列特征最小值，则是最大值。

sklearn中实现了最小-最大缩放，调用MinMaxScaler类即可：

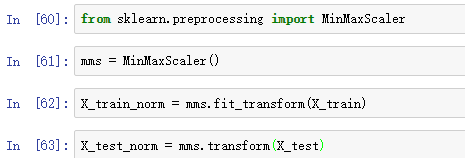
虽然归一化方法简单，但相对来说，标准化对于大部分机器学习算法更实用。原因是大部分线性模型比如逻辑斯蒂回归和线性SVM在初始化权重参数时，要么选择0要么选择一个接近0的随机数。实用标准化，我们能将特征值缩放到以0为中心，标准差为1，换句话说，标准化后的特征形式服从正态分布，这样学习权重参数更容易。此外，标准化后的数据保持了异常值中的有用信息，使得算法对异常值不太敏感，这一点归一化就无法保证。

标准化的计算公式如下：

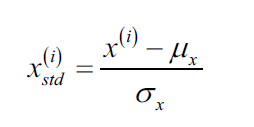
此时，是训练集对应特征列的平均值，是对应特征列的标准差。

下面一张表使用一个简单的例子，展示了标准化和归一化的区别：

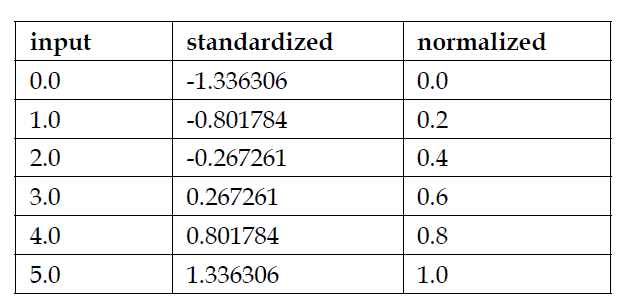
sklearn中提供了StandardScalar类实现列标准化：

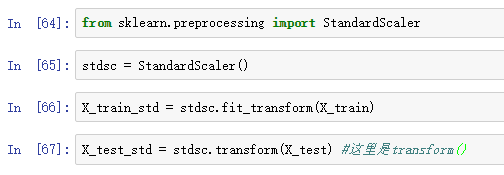
再次强调，StandardScaler只使用训练集fit一次，这样保证训练集和测试集使用相同的标准进行的特征缩放。