透过人工神经元一窥早期机器学习历史
在我们讨论感知机及其相关算法细节前,先让我们回顾一下机器学习早期的发展历程。为了理解大脑工作原理进而设计人工智能,Warren McCullock和Walter Pitts 在1943年首次提出了一个简化版大脑细胞的概念,即McCullock-Pitts(MCP)神经元(W.S.McCulloch and W.Pitts. A Logical Calculus of the Ideas
Immanent in Nervous Activity.)。神经元是大脑中内部连接的神经细胞,作用是处理和传播 化学和电信号,可见下图:
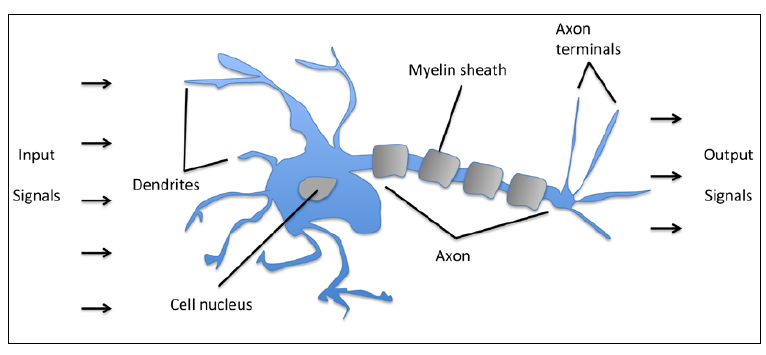
McCullock和Pitts描述了如下的神经细胞:可以看做带有两个输出的简单逻辑门;即有多个输入传递到树突,然后在神经元内部进行输入整合,如果累积的信号量超过某个阈值,会产生一个输出信号并且通过轴突进行传递。 十几年后,基于MCP神经元模型,Frank Rosenblatt发表了第一个感知机学习规则(F.Rosenblatt, The Perceptron, a Perceiving and Recognizing Automaton. Cornell Aeronautical Laboratory, 1957)。 基于此感知机规则,Rosenblatt提出了能够自动学习最优权重参数的算法,权重即输入特征的系数。在监督学习和分类任务语境中,上面提到的算法还能够用于预测一个样本是属于类别A还是类别B。
更准确的描述是,我们可以将上面提到的样本属于哪一个类别这个问题称之为二分类问题(binary classification task),我们将其中涉及到的两个类别记作1(表示正类)和-1(表示负类)。我们再定义一个称为激活函数(activation function) 的东东,激活函数接收一个输入向量
和相应的权重向量
的线性组合,其中
也被称为网络输入(
):
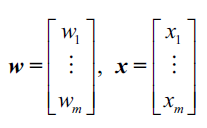
此时,如果某个样本的激活值,即
大于事先设置的阈值
,我们就说样本
属于类别1,否则属于类别-1。
在感知机学习算法中,激活函数的形式非常简单,仅仅是一个单位阶跃函数(也被称为Heaviside阶跃函数):
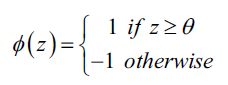 为了推导简单,我们可以将阈值
为了推导简单,我们可以将阈值挪到等式左边并且额外定义一个权重参数
, 这样我们可以对
给出更加紧凑的公式
,此时
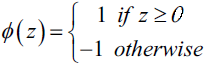
下面左图描述了感知机的激活函数怎样将网络输入压缩到二元输出(-1,1),右图描述了感知机如何区分两个线性可分的类别。
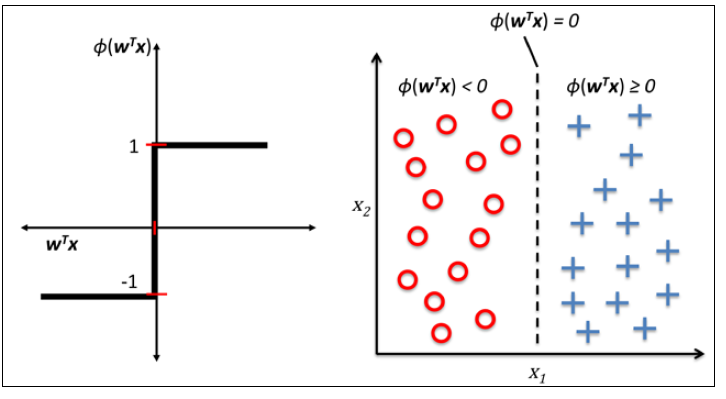
不论MCP神经元还是Rosenblatt的阈值感知机模型,他们背后的idea都是试图使用简单的方法来模拟大脑中单个神经元的工作方式:要么传递信号要么不传递。因此,Rosenblatt最初的感知机规则非常简单,步骤如下:
- 将权重参数初始化为0或者很小的随机数。
- 对于每一个训练集样本
,执行下面的步骤:
- 对于每一个训练集样本
- 1、计数输出值
.
- 1、计数输出值
- 2、更新权重参数.
此处的输出值就是单位阶跃函数预测的类别(1,-1),参数向量中的每个
的更新过程可以用数学语言表示为:
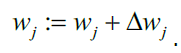
其中,用于更新权重
,在感知机算法中的计算公式为:
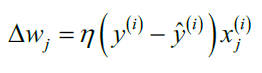 其中
其中 称为学习率(learning rate), 是一个介于0.0和1.0之间的常数,
是第i个训练样本的真实类别,
是对第i个训练样本的预测类别。 权重向量中的每一个参数w_{j}是同时被更新的,这意味着在所有的
计算出来以前不会重新计算
(译者注:通俗地说,我们在计算出一个
,然后同时更新w中的每一个权重参数;然后不断重复上面的步骤)。具体地,对于一个二维数据集,我们可以将更新过程写为:
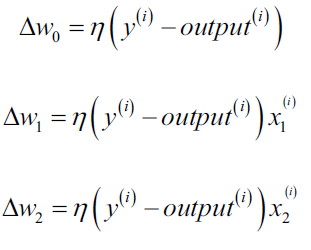
在我们用Python实现感知机算法之前,我们先来草算一下这个简单的算法是多么美妙。如果感知机预测的类别正确,则权重参数不做改变,因为:
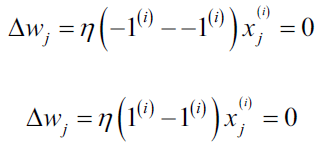 当预测结果不正确时,权重会朝着正确类别方向更新(译者注:如果正确类别是1,权重参数会增大;如果正确类别是-1,权重参数会减小):
当预测结果不正确时,权重会朝着正确类别方向更新(译者注:如果正确类别是1,权重参数会增大;如果正确类别是-1,权重参数会减小):
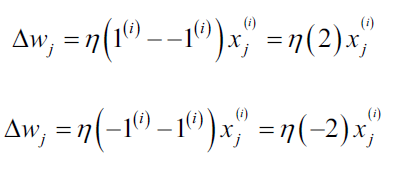
我们可以具体化上面的乘数,比如一个简单的例子:
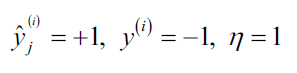
假设,我们将样本误分类为-1.此时,更新过程会对权重参数加1,下一次在对样本i计算输出值时,有更大的可能输出1:
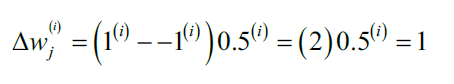
参数更新和样本
成正比。比如,如果我们有另一个样本
=2 被误分类为-1,在更新
时会朝着正确方法更新更多(相比较
=0.5的情况):
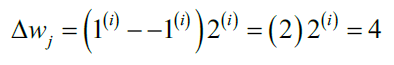
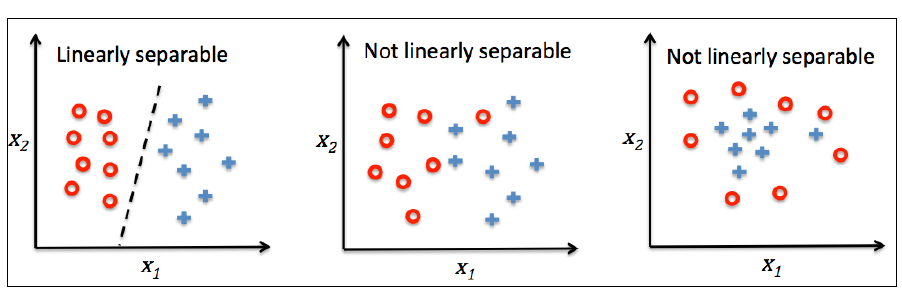
感知机算法仅在两个类别确实线性可分并且学习率充分小的情况下才能保证收敛。如果两个类别不能被一个线性决策界分开,我们可以设置最大训练集迭代次数(epoch)或者可容忍的错误分类样本数 来停止算法的学习过程。
在进入下一节的代码实现之前,我们来总结一下感知机的要点:
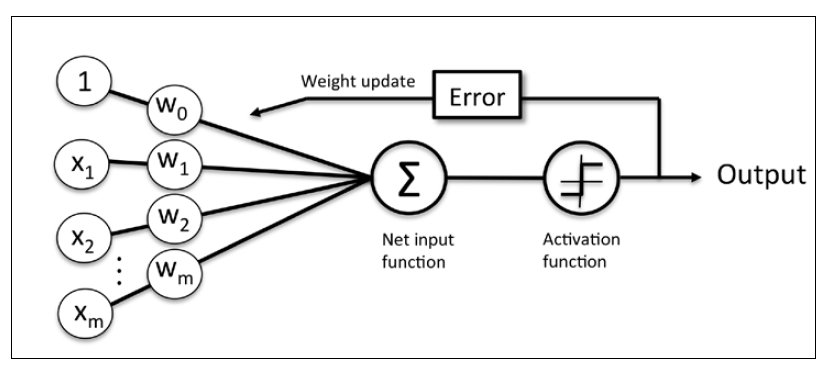
感知机接收一个样本输入x,然后将其和权重w结合,计算网络输入z。z接着被传递给激活函数,产生一个二分类输出-1或1作为预测的样本类别。在整个学习阶段,输出用于计算预测错误率(y-)和更新权重参数。