逻辑斯蒂回归对类别概率建模

感知机算法为我们学习机器学习分类问题曾经立下汗马功劳，但由于其致命缺点：如果数据不能完全线性分割，则算法永远不会收敛。我们实际上很少真正使用感知机模型。

接下来我们学习另一个非常有效的线性二分类模型：逻辑斯蒂回归(logistic regression)。注意，尽管模型名字中有“回归”的字眼，但她确是百分百的分类模型。

逻辑斯蒂回归和条件概率

逻辑斯蒂回归(以下简称逻辑回归)是一个分类模型，它易于实现，并且对于线性可分的类别数据性能良好。她是工业界最常用的分类模型之一。和感知机和Adaline相似，本章的逻辑回归模型也是用于二分类的线性模型，当然可以使用OvR技巧扩展为多分类模型。

逻辑回归作为一个概率模型，为了解释其背后的原理，我们先介绍一个概念：几率(odds ratio)=, 其中p表示样本为正例的概率。这里如何划分正例、负例要根据我们想要预测什么，比如，我们要预测一个病人有某种疾病的概率，则病人有此疾病为正例。数学上，正例表示类别y=1。有了几率的概念，我们可以定义对数几率函数(logit function,这里log odds简称logit)：

对数几率函数的自变量p取值范围[0,1],因变量值域为实数域，将上式中的p视为类后验概率估计p(y=1|),然后定义如下线性关系：

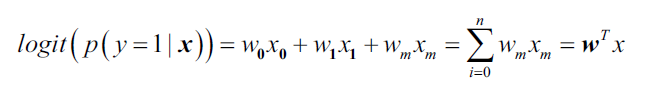
实际上我们关心的是某个样本属于类别的概率，恰恰是对数几率函数的反函数，也被称为逻辑斯底函数(logistic function)，有时简写为sigmoid函数，函数图像是S型：

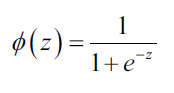其中z是网络输入，即权重参数和特征的线性组合。

sigmoid(S曲线)函数很重要，我们不妨画图看一看：

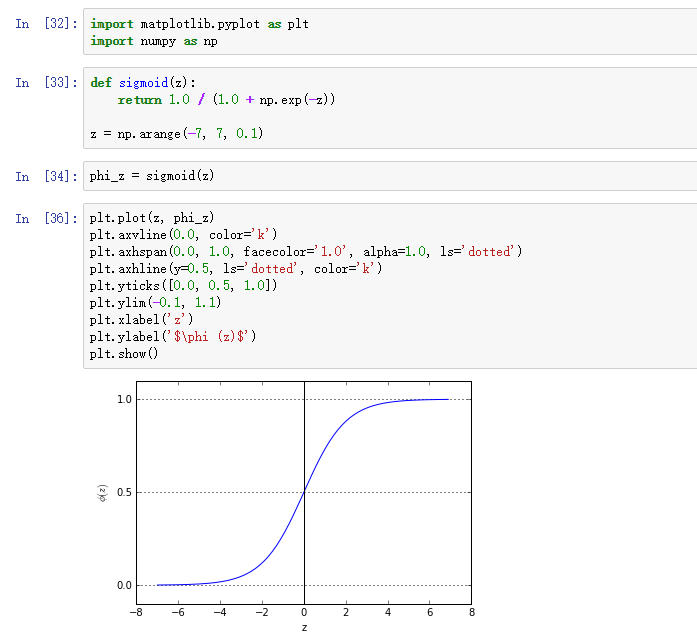
我们可以看到随着z趋向正无穷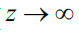，无限接近于1；z趋向负无穷，无限接近0.因此，对于sigmoid函数，其自变量取值范围为实数域，因变量值域为[0,1],并且sigmoid(0)=0.5。

为了直观上对逻辑回归有更好的理解，我们可以和Adaline模型联系起来，二者的唯一区别是：Adaline模型，激活函数，在逻辑回归中，激活函数变成了sigmoid函数。

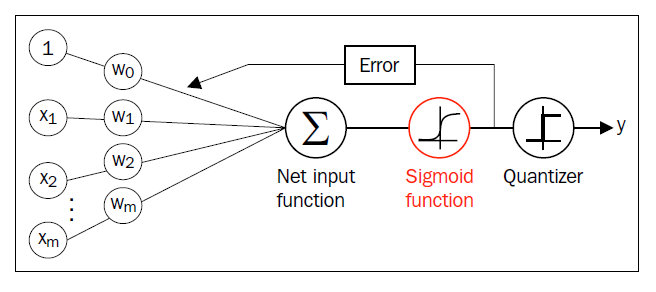
由于sigmoid函数的输出是在[0,1]，所以可以赋予物理含义：样本属于正例的概率，。举例来说，如果，意味着此样本是Iris-Versicolor花的概率是0.8，是Iris-Setosa花的概率是。

有了样本的预测概率，再得到样本的类别值就很简单了,和Adaline一样，使用单位阶跃函数：

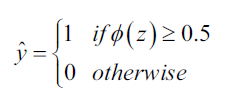
上式等价于：

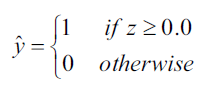
逻辑回归之所以应用广泛，一大优点就是它不但能预测类别，还能输出具体的概率值，概率值很很多场景往往比单纯的类别值重要的多。比如在天气预测中下雨的可能性，病人患病的可能性等等。

学习逻辑斯底损失函数中的权重参数

对逻辑回归模型有了基本认识后，我们回到机器学习的核心问题，怎样学习参数。还记得上一章Adaline中我们定义的差平方损失函数：

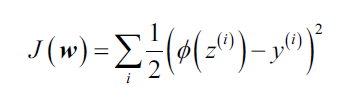
我们求解损失函数最小时的权重参数，同样，对于逻辑回归，我们也需要定义损失函数，在这之前，先定义似然(likelihood)L的概念，假设训练集中样本独立，似然定义：

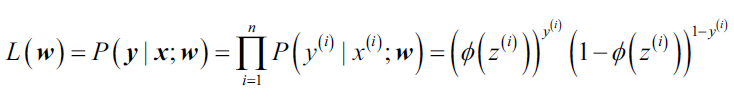与损失函数费尽全力找最小值相反，对于似然函数，我们要找的是最大值。实际上，对于似然的log值，是很容易找到最大值的，也就是最大化log-likelihood函数：

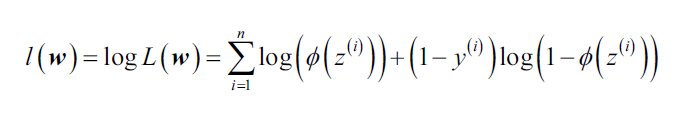
接下来，我们可以运用梯度下降等优化算法来求解最大化log-likelihood时的参数。最大化和最小化本质上没有区别，所以我们还是将log-likelihood写成求最小值的损失函数形式：

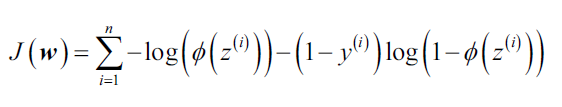
为了更好地理解此损失函数，假设现在训练集只有一个样本：

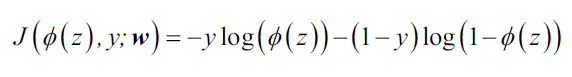
上式等号右边的算式，如果y=0则第一项为0；如果y=1则第二项为0。

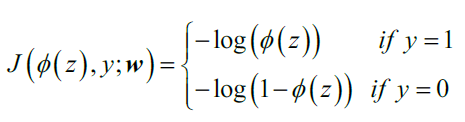
下图展示了一个训练样本时，不同时对应的:

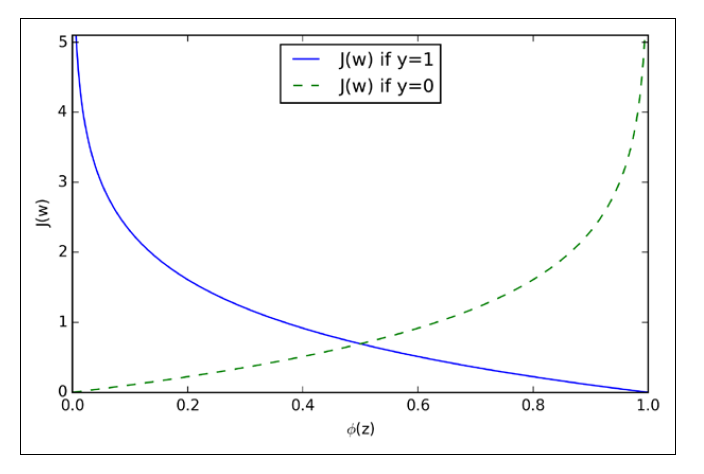
对于蓝线，如果逻辑回归预测结果正确，类别为1，则损失为0；对于绿线，如果逻辑回归预测正确，类别为0，则损失为0。 如果预测错误，则损失趋向正无穷。

调用scikit-learn训练逻辑回归模型

如果我们自己实现逻辑回归，只需要将第二章中的Adaline中的损失函数替换掉即可，新的损失函数：

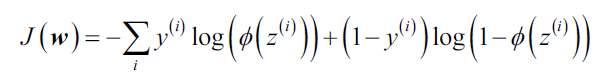
不过考虑到sklearn中提供了高度优化过的逻辑回归实现，同时也支持多类别分类，我们就不自己实现了，而是直接调用sklearn.linear_model.LogisticRegression，使用标准化后的Iris数据集训练模型：

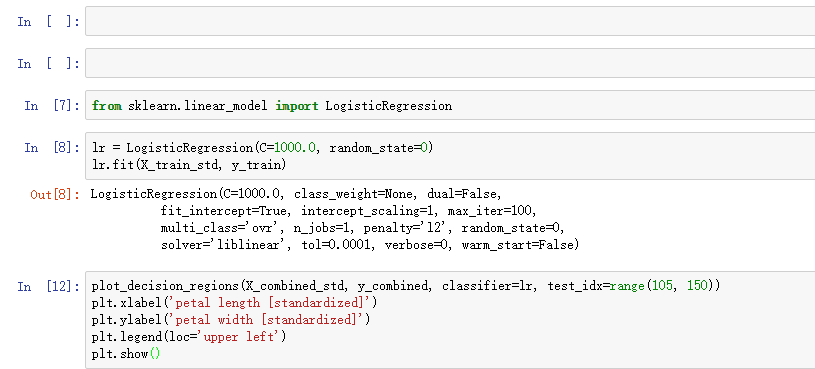
训练模型后，我们画出了决策界，

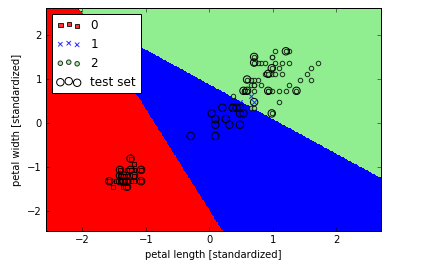
细心的你一定会问在初始化LogisticRegression时那个参数C是什么意思呀？在下一节讲正则化的时候我们再好好讨论讨论。

有了逻辑回归模型，我们就可以预测了，如果你想知道输出概率，调用predict_proba方法即可，

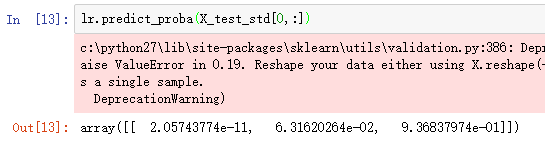
上面的array表示lr认为测试样本属于Iris-Virginica类别的概率为93.683%，属于Iris-Versicolor的概率为6.316%。

不论Adaline还是逻辑回归，使用梯度下降算法更新权重参数时，用到的算式都一样，。

我们好好推导一下这个计算过程，首先计算log-likelihood函数对权重参数的偏导数：

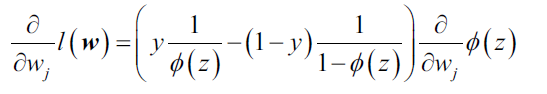
然后，计算sigmoid函数的导数：

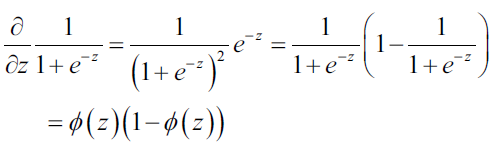
将上式代入到损失函数偏导数：

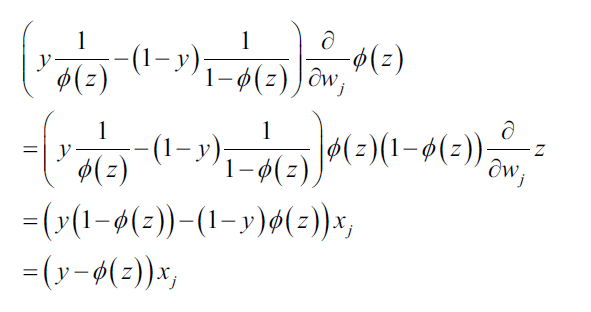
我们的目标是求解使log-likelihood最大值时的参数w，因此，对于参数更新，我们按照：

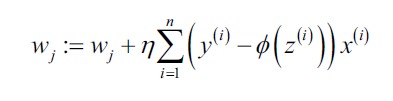
由于每次更新权重时，对于所有参数同时更新，所以可以写成向量形式：

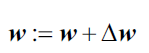
我们定义

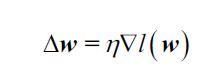
由于最大化log-likelihood等价于最小化损失函数,我们可以将梯度下降算法的权重更新写作：

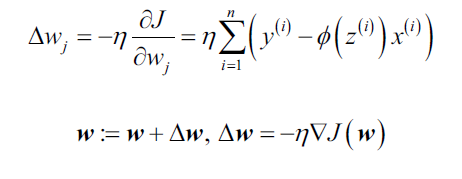
这和Adaline中的权重更新算式完全相同。