随机森林
随机森林一直是广受欢迎的模型,优点很多:优秀的分类表现、扩展性和使用简单。随机森林的思想也不复杂,一个随机森林模型就是多颗决策树的集成。集成学习(ensemble learning)的观点是将多个弱分类器结合来构建一个强分类器,它的泛化误差小且不易过拟合。
随机森林算法大致分为4个步骤:
- 通过自助法(bootstrap)构建大小为n的一个训练集,即重复抽样选择n个训练样例
- 对于刚才新得到的训练集,构建一棵决策树。在每个节点执行以下操作:
- 通过不重复抽样选择d个特征
- 利用上面的d个特征,选择某种度量分割节点
- 重复步骤1和2,k次
- 对于每一个测试样例,对k颗决策树的预测结果进行投票。票数最多的结果就是随机森林的预测结果。至于如何投票,下面会讲到。
随机森林中构建决策树的做法和原始决策树的区别是,在每次分割节点时,不是从所有特征中选择而是在一个小特征集中选择特征。
虽然随机森林模型的可解释性不如决策树,但是它的一大优点是受超参数的影响波动不是很大(译者注:几个主要参数还是需要好好调参的)。我们也不需要对随机森林进行剪枝因为集成模型的鲁棒性很强,不会过多受单棵决策树噪音的影响。
在实际运用随机森林模型时,树的数目(k)需要好好调参。一般,k越大,随机森林的性能越好,当然计算成本也越高。
样本大小n能够控制bias-variance平衡,如果n很大,我们就减小了随机性因此随机森林就容易过拟合。另一方面,如果n很小,虽然不会过拟合,但模型的性能会降低。大多数随机森林的实现,包括sklearn中的RandomForestClassifier,n的大小等于原始训练集的大小。
在每一次分割时特征集的大小d,一个最起码的要求是要小于原始特征集大小,sklearn中的默认值,其中m是原始特征集大小,这是一个比较合理的数值。
直接调用sklearn来看一下随机森林吧:

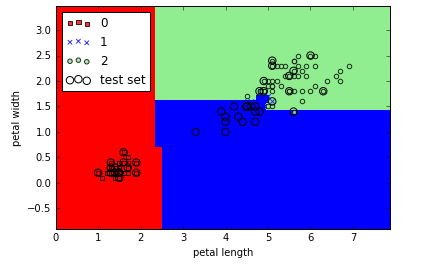
运行上面的代码,我们训练了一个含有10颗树的随机森林,使用熵作为分割节点时的度量。虽然我们在一个小数据集上训练了一个非常小的模型,但我还是使用了n_jobs这个并行化参数,此处使用了计算机的两个核训练模型。